Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 10.Problemas - Ex. 62
Usando o teorema de Thévenin, determine vo no circuito da Figura 10.105.
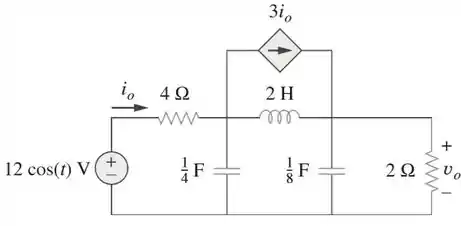
Passo 1
Vamos lá galera! Em questões de Thevenin ou Nortón, um dos macetes mais importantes é saber trabalhar para isolar as fontes e achar as impedâncias equivalentes! Primerio, vamos transformar o circuito para o domínio da frequência!
Passo 2
Para acharmos a impedância equivalente, vamos observar o circuito abaixo!
No nó 1,
No nó 2,
Passo 3
Para acharmos a tensão de Thevenin, consideremos o circuito abaixo:
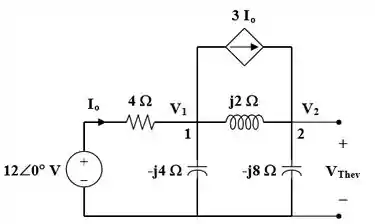
No nó 1,
No nó 2,
Fazendo a matriz para resolver os dois nos, temos:
Passo 4
Portanto,
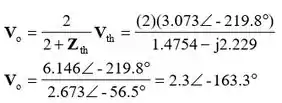
Logo,
Resposta
Exercícios de Livros Relacionados
Use a análise nodal para calcular o valor de v em regime permanente, se v g = V m cos ω t e calcule a amplitude de v para os casos de ω = (a) 0 , (b) 1000 e (c) 10 6 rad/s. Compare o resultado para
Calcule a tensão v em regime permanente, usando análise nodal.
Calcule a corrente i em regime permanente.
Calcule a tensão v em regime permanente.
Calcule a tensão v em regime permanente, se v g = 2 cos 2 tV .