Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 17.Problemas - Ex. 5

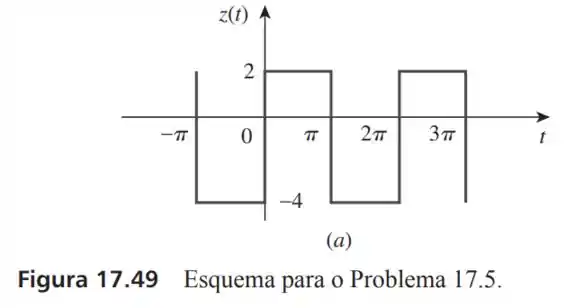
5- Obtenha a expansão em série de Fourier para a forma de onda mostrada na Figura 17.49 .

Passo 1

O período de onda dessa função é de:

T = 2 π

Então o ω dessa onda será:

ω = 2 π T = 2 π 2 π = 1

E as funções dentro do período de 0 até 2 π são:

f t = 2 → 0 < t < π

f t = - 4 → π < t < 2 π

Passo 2

E o valor de a o será:

a o = 1 T ∫ 0 π 2   d t + ∫ π 2 π - 4 d t

a o = 1 2 π 2 π + - 8 π + 4 π

a o = - 2 π 2 π = - 1

Passo 3

Agora o valor de a n :

a n = 2 2 π ∫ 0 π 2 cos ⁡ n t d t + ∫ π 2 π - 4 cos ⁡ n t   d t

a n = 1 π 2 n sin ⁡ n t 0 π - 4 n sin ⁡ n t π 2 π

a n = 2 n π sin ⁡ π n - sin ⁡ 0 - 2 sin ⁡ 2 π n + 2 sin ⁡ π n

Onde para n sendo um número inteiro temos:

sin ⁡ 0 = sin ⁡ π n = sin ⁡ 2 π n = 0

Então:

a n = 0

Passo 4

Agora para b n :

b n = 2 2 π ∫ 0 π 2 sin ⁡ n t d t + ∫ π 2 π - 4 sin ⁡ n t   d t

b n = 1 π 2 n - cos ⁡ n t 0 π - 4 n - cos ⁡ n t π 2 π

Então:

b n = 2 π n - cos ⁡ π n + cos ⁡ 0 + 2 cos ⁡ 2 π n - 2 cos ⁡ π n

b n = 2 π n - cos ⁡ π n + 1 + 2 cos ⁡ 2 π n - 2 cos ⁡ π n

Pode se entender a função :

cos ⁡ π n = - 1 n

Colocando todos esses parâmetros na sérei de Fourier para 100 pontos nós temos:

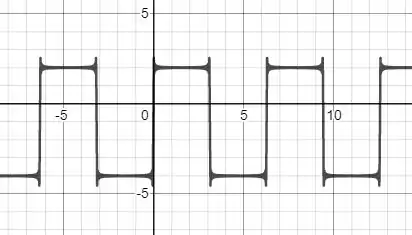
O que nos diz que estamos certos.

Resposta

a o = - 1

a n = 0

b n = 2 π n - cos ⁡ π n + 1 + 2 cos ⁡ 2 π n - 2 cos ⁡ π n

Ver Outros Exercícios desse livro