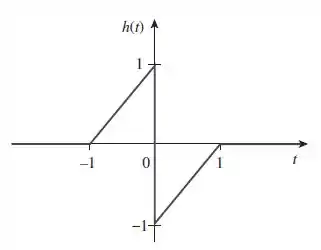
Obtenha a transforma de Fourier o sinal indicado na Figura .
Passo 1
Galerinha, podemos expressar essa função da seguinte maneira:
A primeira derivada é dada por:
E a segunda derivada é:
Aplicando a transformada de Fourier dos dois lados usando a propriedade da derivada:
Passo 2
Vamos usar as seguintes relações trigonométricas exponenciais:
Assim,
Resposta
A transformada é igual a: