Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 17.Problemas - Ex. 42

A onda quadrada da Figura 17.78 a é aplicada ao circuito da Figura 17.78 b . Determine a série de Fourier de v 0 ( t ) .

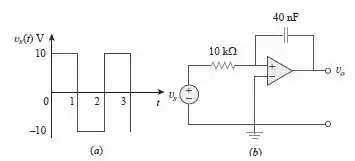
Passo 1

Vamos lá, galera! Bom, a série de Fourier para uma onda quadrada pode ser obtida da tabela 17.3 , que é igual a:

v s t = 40 π ∑ n = 1 ∞ 1 2 n - 1 s e n ( 2 n - 1 ω 0 t )

onde ω 0 = 2 π 2 = π .

Precisamos transformar os elementos do circuito do domínio do tempo para o domínio da frequência. Para ω n = 2 n - 1 ω 0 = 2 n - 1 π ,

10   k Ω   →     10   k Ω

40   n F   →   1 j 2 n - 1 ω 0 C = 25 × 10 6 j 2 n - 1 π

Passo 2

Vamos encontrar a resposta dos equipamentos CC e CA. A tensão de saída V 0 pode ser obtida por:

V 0 = - 1 j 2 n - 1 ω 0 R C V s

V 0 = - 2500 j 2 n - 1 π V s … ( 1 )

  • Componente de corrente contínua

    • Como o valor médio de V s é zero, a saída CC também será zero:

    V c c = 0

  • Componente de corrente alternada

Expressando a equação ( 1 ) e a componente CA de V s na forma polar, temos:

V c a = 2500 ∠ π 2 n - 1 π ∠ π 2 × 40 π ( 2 n - 1 ) ∠ - π 2

V c a = 10 5 π 2 2 n - 1 2 ∠ 0

Passo 3

Para encontrarmos V 0 , basta somarmos V c c e V c a . Assim,

V 0 = V c c + V c a

V 0 = 0 + 10 5 π 2 2 n - 1 2

Convertendo o resultado para o domínio do tempo,

v 0 t = ∑ n = 1 ∞ 10 5 π 2 2 n - 1 2 c o s ⁡ ( 2 n - 1 π t )

Resposta

A série é igual a:

v 0 t = ∑ n = 1 ∞ 10 5 π 2 2 n - 1 2 c o s ⁡ ( 2 n - 1 π t )

Ver Outros Exercícios desse livro