Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 17.Problemas - Ex. 75

Projete um filtro R C passa-baixas com uma resistência R = 2 k Ω . A entrada para o filtro é um trem de pulsos retangular periódico (ver Tabela 17.3) com A = 1 V ,   T = 10 m s   e   τ = 1 m s . Escolha C de tal forma que a componente C C da saída seja 50 vezes maior que a componente fundamental da saída.

Passo 1

Nosso filtro R C passa-baixas padrão será dado por

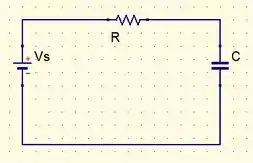
Para o nosso caso temos que v s pode ser expresso como

v s = A τ T + 2 A T ⋅ ∑ n = 1 ∞ 1 n ⋅ sin ⁡ n π τ T ⋅ cos ⁡ ( n ⋅ ω 0 t )  

Se denominarmos por v 0 a tensão no capacitor vamos, a partir da utilização de um divisor de tensão, encontrar a seguinte expressão para v 0

v 0 = 1 j ω n ⋅ C R + 1 j ω n ⋅ C ⋅ v s = 1 1 + j ω n ⋅ R C ⋅ v S ,     ω n = n ω 0 = 2 π n T

Passo 2

Continuando com nossa resolução se tivermos n = 0 → V 0 = V s = A τ / T     i (componente dc) para o e-nésimo harmônico teremos

V 0 = 1 1 + ω n 2 ⋅ R 2 C 2 ∠ arctan ⁡ ω n R C ⋅ 2 A n T ⋅ sin ⁡ n π τ T ∠ - 90 °

Quando tivermos n = 1

→ V 0 = 2 A T ⋅ sin ⁡ n π τ T ⋅ 1 1 + 4 π 2 T ⋅ R 2 C 2             i i

A partir de i e i i vamos encontrar

A τ T = 50 ⋅ 2 A T ⋅ sin ⁡ π 10 ⋅ 1 1 + 4 π 2 T ⋅ R 2 C 2 → 1 + 4 π 2 T ⋅ R 2 C 2 = 30.9 τ

1 + 4 π 2 T ⋅ R 2 C 2 = 3.09 ⋅ 10 4 → 1 + 4 π 2 T ⋅ R 2 C 2 ≈ 10 10 →

→ C = T 2 π R ⋅ 10 5 = 10 - 2 ⋅ 3.09 ⋅ 10 4 4 π ⋅ 10 3   24.59   m F

Resposta

C = 24.59   m F

Ver Outros Exercícios desse livro