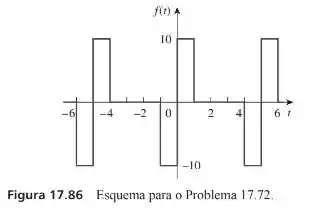
O sinal exibido por um aparelho médico pode ser aproximado pela forma de onda mostrada na Figura 17.86. Determine a representação em série de Fourier do sinal.

Temos que nossa forma de onde é periódica, assim, podemos identificar algumas grandezas que nos serão importantes. São elas

Além disso, podemos perceber que nossa função é anti-simétrica em relação à origem. Sendo assim, nossa função será uma função ímpar o que implica que teremos . Portanto, resta-nos calcular quem é para encontrarmos a representação em série de Fourier para a nossa forma de onda, então,

Portanto, nossa representação em série de Fourier será dada por