Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 6.Problemas - Ex. 2a

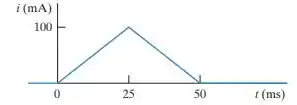
O pulso triangular de corrente mostrado na Figura P6.2 é aplicado a um indutor de 500 mH.

a) Escreva as expressões que descrevem i(t) nos quatro i n t e r v a l o s   t   ,   0 ,   0 ≤   t < -   25   m s ,   25   m s ≤   t ≤   50   m s   e   t   .   50   m s .  

b) Deduza as expressões para a tensão, potência e energia do indutor. Use a convenção passiva.

Passo 1

Falaiii meus xuxu’s, ceis tão bonzinho??

Espero que sim hein, bora lá pra mais uma?

Encostaaaa

  1. Partindo do pulso de corrente triangular, pode –se observar que não há corrente no indutor para t < 0

Por isso

i t = 0 A         p a r a   t < 0

Portanto, a expressão para i t no intervalo de tempo t < 0     é     i t = 0 A

Passo 2

Para o intervalo de tempo 0 ≤ t ≤ 25   m s , a forma de onda da corrente através do indutor é uma rampa positiva. A expressão para este sinal de rampa é calculada da seguinte maneira:

O ponto inicial da rampa positiva é ( x 2   ,   y 2   ) = ( 0   m s ,   0   m A )

O ponto final da rampa positiva é   ( x 2   ,   y 2   ) = ( 25   m s , 10 0   m A )

Agora a equação da linha que une acima de dois pontos, é

y - y 1 = y 2 - y 1 x 2 - x 1 ( x - x 1 )

i t - 0 = 100 × 10 - 3 - 0 25 × 10 - 3 - 0 ( t - 0 )

i t = 4 t   A

Portanto, a expressão para i ( t ) no intervalo 0 ≤ t ≤ 25   m s é

i t = 4 t   A

Passo 3

Para o intervalo de tempo 25 ≤ t ≤ 5 0   m s , a forma de onda da corrente através do indutor é uma rampa positiva. A expressão para este sinal de rampa é calculada da seguinte maneira:

O ponto inicial da rampa positiva é ( x 2   ,   y 2   ) = ( 25   m s ,   10 0   m A )

O ponto final da rampa positiva é   ( x 2   ,   y 2   ) = ( 5 0   m s , 0   m A )

Agora a equação da linha que une acima de dois pontos, é

y - y 1 = y 2 - y 1 x 2 - x 1 ( x - x 1 )

i t - 10 0 × 10 - 3 = 0 - 100 × 10 - 3 50 × 10 - 3 - 25 × 10 - 3 - 0 ( t - 25 × 10 - 3 )

i t = 0.1 - 4 ( t - 0.025 )   A

i t = 0.2 - 4 t   A

Portanto, a expressão para i ( t ) no intervalo 25 ≤ t ≤ 5 0   m s é

i t = 0.2 - 4 t   A

Para o intervalo de tempo t > 50   m s , a corrente através do indutor é zero

Portanto, a expressão para i ( t ) no intervalo t > 50 m s é

i t = 0 A

Portanto, as expressões para a corrente do indutor são

i t = 0   A                             p a r a               t < 0 4 t   A                                         p a r a   0 ≤ t ≤ 25   m s 0.2 - 4 t   A           p a r a   25 m s ≤ t ≤ 50   m s 0   A                                     p a r a   t > 50   m s

Resposta

i t = 0   A                             p a r a               t < 0 4 t   A                                         p a r a   0 ≤ t ≤ 25   m s 0.2 - 4 t   A           p a r a   25 m s ≤ t ≤ 50   m s 0   A                                     p a r a   t > 50   m s

Exercícios de Livros Relacionados

Os indutores da figura 6.87 são incialmente carregados e conectados à caixa preta em t = 0 . Se i 1 0 = 4 A ,i 2 0 = - 2 Aev t = 50 e - 200 tm V para t ≥ 0 , determine: a A energia inicialmente armaze
A corrente i t através de um indutor de 20m H é igual, em magnitude, à tensão nele para todos os valores de tempo. Se i 0 = 2 A , determine i t .
Elabore um problema que ajude outros estudantes a entenderem melhor como os capacitores funcionam juntos quando conectados em série e paralelo.
Determine a capacitância equivalente.
A capacitância equivalente nos terminais a-b no circuito da figura abaixo é 30μ F . Calcule o valor de C.