Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 6.Problemas - Ex. 65

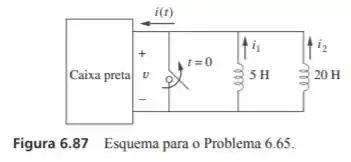
Os indutores da figura 6.87 são incialmente carregados e conectados à caixa preta em t = 0 . Se i 1 0 = 4 A ,   i 2 0 = - 2 A   e   v t = 50 e - 200 t   m V para t ≥ 0 , determine:

a A energia inicialmente armazenada em cada indutor.

b A energia total liberada para a caixa preta de t = 0 e t = ∞ .

c i 1 t   e   i 2 t ,   t ≥ 0 .

d i t ,   t ≥ 0 .

Passo 1

Como o enunciado trata de energia armazenada em um indutor devemos nos lembrar que esse componente de circuito é regido pela seguinte equação

w = 1 2 ⋅ L ⋅ i 2   i

Além disso, também devemos nos lembrar que para um indutor a sua corrente não varia instantaneamente e que a equação que o rege primordialmente é

i = 1 L ⋅ ∫ 0 t v t d t + i 0     i i

Passo 2

Sendo assim, podemos calcular a energia acumulada em cada indutor de 5 H   e   20 H denotando por W 5   e   W 20 , respectivamente. Assim, teremos

w 5 = 1 2 ⋅ L ⋅ i 2 = 1 2 ⋅ 5 ⋅ 4 2 = 40 J

w 20 = 1 2 ⋅ L ⋅ i 2 = 1 2 ⋅ 20 ⋅ - 2 2 = 40 J

E, então, temos que a energia total liberada para a caixa preta de t = 0 e t = ∞ será dada pela soma de w 5   e   w 20 ou seja

W = W 5 + W 20 = 80 J

Passo 3

Agora, utilizando a equação número i i podemos encontrar a corrente que passa por cada indutor fazendo

i 1 = 1 L 1 ⋅ ∫ 0 t v t d t + i 1 0 = 1 5 ⋅ 1 200 ⋅ 50 e - 200 t ⋅ 10 - 3 0 t + 4

  i 1 = 5 ⋅ 10 - 5 ⋅ e - 200 t - 1 + 4   A

Repetindo o mesmo processo para i 2 vamos encontrar

i 2 = 1 L 2 ⋅ ∫ 0 t v t d t + i 2 0 = 1 20 ⋅ 1 200 ⋅ 50 e - 200 t ⋅ 10 - 3 0 t - 2  

i 2 = 1.25 ⋅ 10 - 5 ⋅ e - 200 t - 1 - 2   A

Por fim, para concluirmos o exercício devemos encontrar o valor de i ( t ) que vai ser dado pela soma de i 1   com i 2 . Portanto,

i t = i 1 t + i 2 t =   5 ⋅ 10 - 5 ⋅ e - 200 t - 1 + 4   + 1.25 ⋅ 10 - 5 ⋅ e - 200 t - 1 - 2  

i t = 6 . 25 ⋅ 10 - 5 ⋅ e - 200 t - 1 + 2   A  

Resposta

a   W 5 = 40 J   e   W 20 = 40 J

b   w = 80 J

c   i 1 = 5 ⋅ 10 - 5 ⋅ e - 200 t - 1 + 4   A   e   i 2 = 1.25 ⋅ 10 - 5 ⋅ e - 200 t - 1 - 2   A

d   i = 6.25 ⋅ 10 - 5 ⋅ e - 200 t - 1 + 2   A  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A tensão em um capacitor de 5mF é mostrada na figura abaixo. Determine a corrente através do capacitor.
Uma corrente de 4 sin ⁡ 4 tA passa por um capacitor de 5F. Descubra a tensão v(t) no capacitor, dado que a tensão inicial é de 1 V.
Um capacitor de 4mF apresenta a seguinte tensão em seus terminais. v =50V ,t ≤ 0 Ae - 100 t + B e - 600 t ,t ≥ 0 Se o capacitor tiver uma corrente inicial de 2A, determine a corrente no capacitor para
A forma de onda da tensão apresentada na figura abaixo é aplicada em um capacitor de 55μ F . Desenhe a forma de onda da corrente que passa por ele.
Um capacitor de 50μ F possui energia w t = 10c o s ² 377 tJ ² . Determine a corrente que passa pelo capacitor.