Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 6.Problemas - Ex. 16

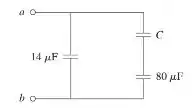
A capacitância equivalente nos terminais a-b no circuito da figura abaixo é 30   μ F . Calcule o valor de C.

Passo 1

Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos pede para dizer qual será o valor do capacitor dali com a capacitância equivalente final dada. Parece muita coisa, mas é tranquilo. Partiu??

Passo 2

Bom, nosso primeiro passo vai ser pensar que, por ser um capacitor, sua capacitância equivalente em série é calculada da mesma forma que a resistência equivalente em paralelo (multiplicação dos fatores em cima e soma embaixo).

C s = C   x   8 0 80 + C

Passo 3

E a nossa capacitância equivalente em paralelo é calculada seguindo os passos da resistência equivalente em série, ou seja, soma tudo o que tiver de capacitância ali.

C p = 14 + C   x   80 80 + C

30 = 14 + C   x   80 80 + C

C = 2 0   μ F

Resposta

C = 20   μ F

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Se a forma de onda da tensão na figura 6.68 for aplicada a um indutor de 10 m H , determine a corrente i t . Suponha i 0 = 0 .
A corrente através de um indutor 12 m H é 4 ⋅ sin ⁡ 100 tA . Determine a tensão, no indutor no intervalo π 200s e a energia armazenada em t = π 200s .
Um indutor de 100 m H é conectado em paralelo com um resistor de 2 k Ω . A corrente que passa pelo indutor é i t = 50 ⋅ e - 400 t m A . a Determine a tensão v l no indutor. b Determine a tensão v r no
Se a forma de onda da tensão na figura 6.67 for aplicada aos terminais de um indutor de 5 H , calcule a corrente através do indutor. Suponha i 0 = - 1 A .
Em condições CC de regime estacionário, determine i e v no circuito da figura 6.71.