Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 5.2 - Ex. 1
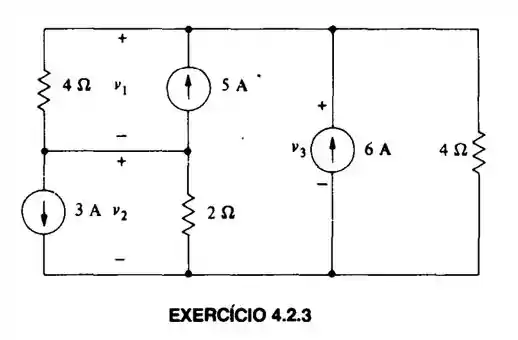
Resolva o Exerc. 4.2.3 usando superposição.
Passo 1
E aí, galerinha! Tudo tranks? Simbora pra mais uma aí!?
Bom! A questão pede pra gente resolver o problema usando superposição.!
Temos três fontes de corrente aí... E o objetivo do Exercício 4.2.3 é achar o valor de , e ...
Pois muito bem! Pra resolver esse exercício vamos considerar cada uma das três fontes isoladamente, e aí a gente vai obtendo , e pra cada uma dessas três situações. No final, é só somar!
Passo 2
Para a primeira parte, vamos excluir as fontes de e ... Com isso, temos que...
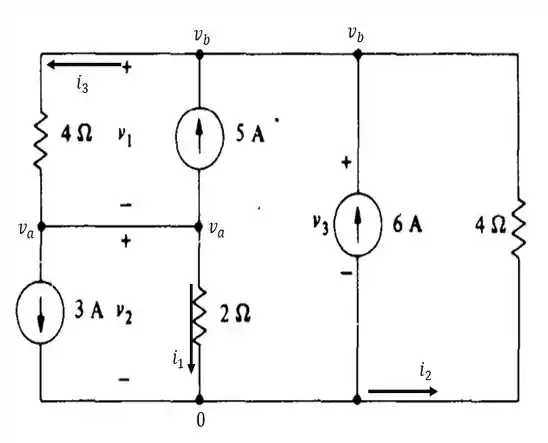
Aplicando a ...
Passo 3
E depois, recorrendo à análise nodal para essas duas equações, obtemos que...
Somando as duas equações...
E então, é dado por...
Aí, pelo que vemos do esboço que fizemos, as tensões , e são dadas em função de e por...
Pronto, galerinha! Finalizamos aqui!