Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 11.Problemas - Ex. 38
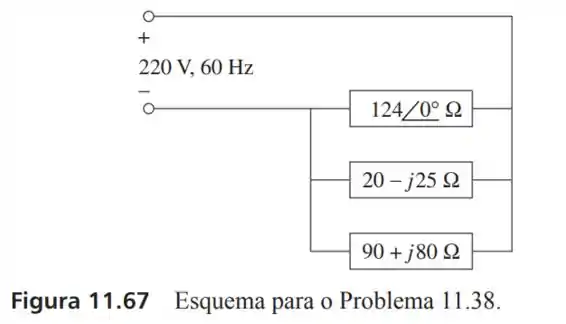
38- Para o sistema de potência da Figura , determine: potência média; potência reativa; fator de potência. Note que é uma valor
Passo 1
Vamos calcular a potência total nas três reatâncias e a partir dela aplicar o triângulo de potência.
Sabendo que a potência total é calculada por:
Onde é o conjugado da reatância.
Passo 2
Para calcular a potência média basta somar os componentes reais das potências totais:
E a potência reativa será a soma de todas as componentes imaginárias da potência real:
Onde a potência deverá ser positiva, então temos que tirar o módulo.
Passo 3
Para saber o fator de potência nós deveremos saber o cosseno ângulo de fase desse sistema. E para saber o ângulo de fase temos que fazer:
E o cosseno desse ângulo nos dará:
Resposta
Exercícios de Livros Relacionados
48- Determine a potência complexa para os seguintes casos: ( a ) P = 296W ,Q = 150V A R (capacitivo)
47- Para cada um dos casos a seguir, determine a potência complexa, a potência média e a potência reativa: d I = 10 ∠ 60AR M S ,Z = 100∠ 45 °Ω
48- Determine a potência complexa para os seguintes casos: ( b ) Q = 2000V A R ,F P = 0.9 (adiantado)
41- Obtenha o fator de potência para cada um dos circuitos da Figura 11.68 . Especifique se cada fator de potência está adiantado ou atrasado.
49- Determine a potência complexa para os seguintes casos: c ) V R M S = 208∠ 20 °V ,I R M S = 6.5∠ - 50°A