Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 11.Problemas - Ex. 41a
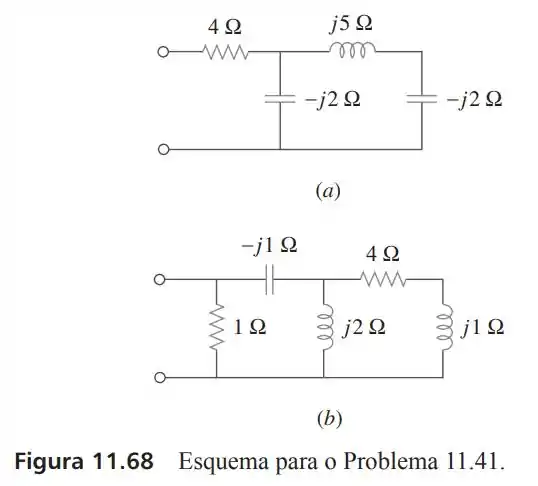
41- Obtenha o fator de potência para cada um dos circuitos da Figura . Especifique se cada fator de potência está adiantado ou atrasado.
Passo 1
Note que as reatâncias e estão em série (assim como fazemos com resistências em circuito ) e a impedância equivalente será igual a:
Isso deixa o circuito da seguinte forma:
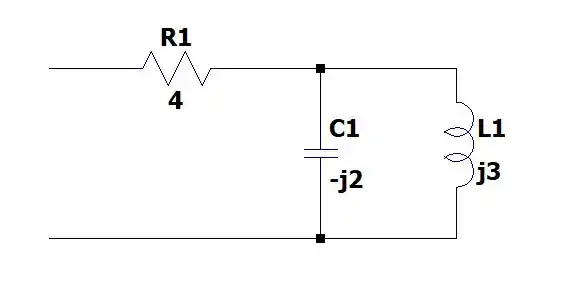
Aí temos que fazer a reatância em paralelo de com e somar com a resistência de . Nos dando uma impedância total de:
Passo 2
O fator de potência será igual a:
Por ter um ângulo negativo, então podemos dizer que a reatância tem característica capacitiva e o capacitor tende a nos dar uma corrente adiantada em relação a tensão, logo o fator de potência está adiantado.
Resposta
Fator de Potência adiantado.
Exercícios de Livros Relacionados
Calcule as impedâncias para as cargas no Ex. 12.5.1, se V e f i c a z = 240V
12.6. Calcule a potência media absorvida pelo resistor de 6-Ω.
Calcule a potência ativa, a potência reativa e a potência complexa entregue pela fonte.
Calcule a leitura do wattímetro
Calcule a potência média entregue ao resistor R