Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 7.Problemas - Ex. 51

Suponha que a chave no circuito da Figura P7.51 esteve na posição a por um longo tempo e que em t = 0 ela é colocada na posição b. Determine (a) vC(0+); (b) vC(q); (c) t para t . 0; (d) i(0+); (e) vC, t $ 0 e (f) i, t $ 0+.

Passo 1

[a] – A polaridade da fonte de tensão está invertida em relação ao capacitor, como esse mesmo capacitor não pode variar tensão instantaneamente, temos:

v c 0 + = - 120   V

Passo 2

[b] – A partir do momento ( t = 0 ), o circuito muda sua configuração, e se mantém desta forma. Portanto, a tensão vai se estabelecer em um valor constante. Esse valor constante vai ser medido por um divisor de tensão.

v c ∞ = 150000 200000 200 = 150   V

Passo 3

[c] – Nesse caso, sai por Thévenin ‘matando’ o capacitor. Logo eu já sei a tensão, já que a mesma não muda

V t h = 150   V

Logo, a resistência equivalente é dada pela combinação de resistores:

R t h = 2500 + 150000 × 50000 150000 + 50000 = 40   k Ω

Então, o circuito equivalente será igual a:

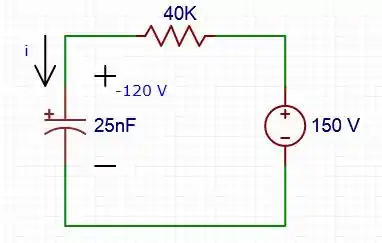
Portanto, já podemos calcular a constante de tempo:

τ = R e q C = 40000 25 × 10 - 9 = 1   m s

Passo 4

[d] – Para o i ( 0 + ) , temos o seguinte equacionamento:

i 0 + = 150 - - 120 40000 = 6,75   m A

Essa corrente entra pelo polo positivo do capacitor, então a ddp vai ser dada pela soma (é necessário fazer uma análise de cada situação) das tensões. Por este motivo, o resultado faz sentido.

Passo 5

[e] – Para o v c , usaremos a equação geral

v c = v c ∞ + v c 0 + - v c ∞ e - t / τ

Substituindo os valores, temos:

v c = 150 + - 120 - 150 e - t τ

v c = 150 - 270 e - 1000 t   V ,     t ≥ 0

Passo 6

[f] – Para o i , pega a fórmula i = C d v c d t que tá tudo certo.

i = C d v C d t

Substituindo os valores:

i = 25 × 10 - 9 - 1000 - 270 e - 1000 t

i = 6,75 e - 1000 t   m A ,     t ≥ 0 +

Resposta

a )   v c 0 + = - 120   V

b )   v C ∞ =   150   V  

c )   τ = 1   m s

d )   i 0 + =   6,75   m A

e )   v c = 150 - 270 e - 1000 t   V ,     t ≥ 0

f )   i = 6,75 e - 1000 t   m A ,     t ≥ 0 +    

Exercícios de Livros Relacionados

As duas chaves mostradas no circuito da Figura P7.17 funcionam simultaneamente. Antes de t = 0, cada chave estava na posição indicada por um longo tempo. Em t = 0, elas passam instantaneamente para su
No circuito mostrado na Figura P7.19, a chave esteve na posição a por um longo tempo. Em t = 0, ela passa instantaneamente de a para b. a) Determine i o (t) para t $ 0. b) Qual é a energia total forne
A fonte de 240 V, e resistência interna de 2 V, no circuito da Figura P7.20, sofre inadvertidamente um curto-circuito em seus terminais a,b. No instante em que a falha ocorre, o circuito estava em fun
Segue o mesmo raciocínio da questão anterior, só que agora quer saber coisas relacionadas a energia armazenada.
A questão quer que o aluno mostre que o resistor tem uma certa equação, e em seguida comparar com o resultado da questão anterior.