Enunciado
Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 4.Problemas - Ex. 54
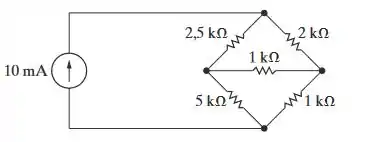
Suponha que lhe pediram para determinar a potência dissipada no resistor horizontal de 1 kV do circuito na Figura P4.54.
a) Qual método de análise de circuitos você recomendaria? Explique por quê.
b) Use o método de análise de sua recomendação para determinar a potência dissipada no resistor horizontal de 1 kV.
c) Você mudaria sua recomendação se o problema fosse determinar a potência gerada pela fonte de corrente de 10 mA? Explique.
d) Determine a potência fornecida pela fonte de corrente de 10 mA.
Passo 1
Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!
A – Primeiramente, o método a ser escolhido é baseado pelo número e o tipo de variáveis desconhecidas, olhando para o circuito, nós temos três nós desconhecidos e duas malhas desconhecidas. Portanto, nós vamos escolher o método das correntes de malha visto que é necessária uma quantidade menor de equações para este caso.
B – Vamos considerar que a corrente na malha triangular superior seja , e na inferior seja , com isso, vamos aplicar o método das correntes de malha na parte triangular superior, com isso
Simplificando a equação, temos
Já aplicando na parte triangular inferior, nós obtemos o seguinte resultado
Logo
Resolvendo o sistema de equações para e , temos
Calculando a potência dissipada em
Substituindo os valores, nós temos que
Portanto
Passo 2
C - Não, o método da corrente de malha ainda seria usado, pois a tensão na fonte de corrente de 10 mA seria calculada usando as correntes de malha. Além disso, resolver duas equações de corrente de malha simultâneas é muito mais fácil do que resolver três equações de tensão de nó.
D – Aplicando o método das correntes de malha na malha à direita, nós temos que
Substituindo os valores e passando para o outro lado,
Logo
Passo 3
Calculando a potência desenvolvida pela fonte de corrente de é igual a
Substituindo os valores, nós temos que
Logo, é igual a