Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 14.Problemas - Ex. 17
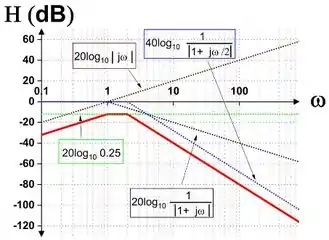
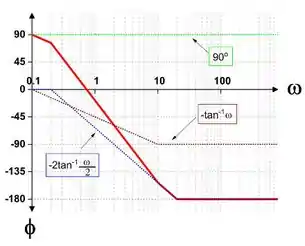
Trace os gráficos de Bode para
Passo 1
Galera, vamos substituir o de acordo com o que foi dado:
A magnitude da função de transferência é:
A fase da função de transferência é:
Desenhando cada termo para a magnitude e a fase e adicionando eles graficamente, conseguimos ter as duas curvas abaixo
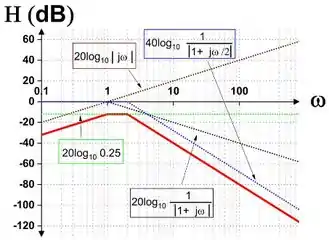
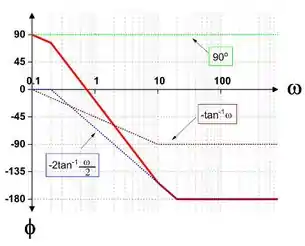
Resposta
Os gráficos são:
