Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 14.Problemas - Ex. 45
Considere o circuito mostrado na Figura e determine , e visto pela tensão no indutor.
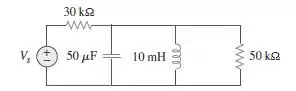
Passo 1
Pessoal, podemos ver que no circuito dado, temos uma fonte de tensão em série com um resistor. Podemos transformar isso numa fonte de corrente em paralelo com o mesmo resistor. Desse modo, teremos uma fonte de corrente e o resistor em paralelo.
Agora que temos dois resistores em paralelo, podemos encontrar o equivalente e nos restará um circuito RLC paralelo!
Passo 2
Para um circuito paralelo, a frequência de ressonância é fácil de ser encontrada!
Substituindo os valores, temos:
Passo 3
A largura de banda pode ser calculada pela seguinte equação:
Substituindo os valores, temos:
Passo 4
Por fim, o fator de qualidade é dado por:
Resposta
Exercícios de Livros Relacionados
A energia inicial no circuito da Figura P13.26 é nula. A fonte de tensão ideal é 600u(t) V. a) Determine Vo(s). b) Use os teoremas dos valores inicial e final para determinar vo(0+) e vo(q). c) Os val
Não há nenhuma energia armazenada no circuito da Figura P13.36 no instante em que a chave é fechada. a) Determine I1. b) Use os teoremas dos valores inicial e final para determinar i 1(0+) e i 1(q). c