Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 12.Problemas - Ex. 32
Três cargas passivas paralelas, estão recebendo potências complexas de valores , respectivamente. Se uma fonte de tensão de é conectada a estas cargas, calcule o valor eficaz da corrente que flui da fonte e o valor de potência visto pela fonte.
Passo 1
Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!
O circuito é dado pela seguinte forma
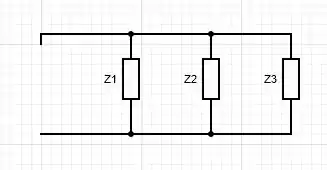
Vamos enumerar as variáveis que nos já foram dadas, que são as seguintes:
Como temos que a potência é igual a
Logo, temos a seguinte configuração
Passo 2
Com isso, a corrente eficaz é igual a
Logo, se temos o conjugado, temos a corrente
Pela equação da potência é igual a
Logo, a potência vista pela fonte é igual a
Resposta
Exercícios de Livros Relacionados
Calcule o valor eficaz de uma corrente periódica para a qual um cicio e dado por:a) i = 3 tA 0 ≤ t ≤ 2 s 0 = 2t ≤ 4 s b) i = 6A0t2 s 0 = 2t8 s c) i = I m sin 2 π t T A 0tT 2 0 = T 2tT s d) i = I m s
Mostre que, para 0 circuito do Ex. 15.4.1, a energia dissipada por ciclo e ∫ 0 2 π w 0 R I M 2 cos 2 w 0 t d t = π R I M 2 w 0 e, desta forma, pela definição (15.27) e 0 resultado do Ex. 15.4.1. que
O amp op no circuito da Figura P10.7 é ideal. Calcule a potência média fornecida ao resistor de 1 kV, quando v g=c o s1.000 tV .