Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 4.Problemas - Ex. 16
Usando a analise nodal, calcule .
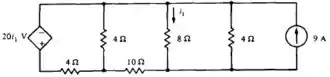
Passo 1
Olá, pessoas!! Sem tomar choque hoje, vamos observar a imagem da questão é fazer as anotações.
;
Passo 2
Vamos montar um sistema...
→
Agora precisamos subtrair as equações do sistema.
→
Passo 3
Com o resultado obtido da subtração do sistema podemos achar .
Com o valor de conseguimos achar , pois é só aplicar o resultado de em qualquer uma das equações do sistema.
Resposta
Como no começo anotamos que , logo concluímos que:
Exercícios de Livros Relacionados
Todas as resistências são de 1 Ω , o elemento w também é um resistor de 1 Ω , os elementos x e y sāo fontes de corrente independentes de 1 A fluindo para cima e o elemento z é uma fonte independente d
Encontre. se for possível, a árvore que contenha todas as fontes de tensão e os ramos cujas tensões controlam fontes dependentes, mas mio contenham fontes de corrente ou ramos cujas correntes controla
12-Use o método das tensões de nó para determinar v1 e v2 no circuito da Figura P4.12.
11-a) Use o método das tensões de nó para determinar as correntes de ramo Ia – Ie no circuito mostrado na Figura P4.11. b) Determine a potência total dissipada no circuito. Figura P4.11
9-Use o método das tensões de nó para determinar a potência que a fonte de 2 A absorve do circuito da Figura P4.9.Fig. P4.9.