Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 6.Problemas - Ex. 8

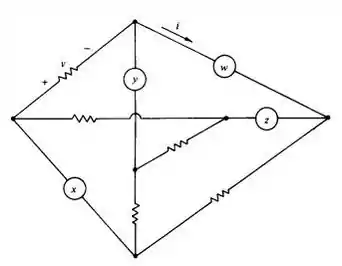
Todas as resistências são de 1 Ω , o elemento w também é um resistor de 1 Ω , os elementos x e y sāo fontes de corrente independentes de 1 A fluindo para cima e o elemento z é uma fonte independente de corrente de 3   A fluindo para a esquerda. Selecionando uma árvore apropriada e usando os métodos da teoria dos gráficos, calcule i . (Note que o circuito é similar ao da Fig. 6.1, e é, entāo, um circuito não-planar. Entretanto, apenas uma equação de laço é necessária neste caso.)

Passo 1

Todas as resistências são de 1 Ω , o elemento w também é um resistor de 1 Ω , os elementos x e y sāo fontes de corrente independentes de 1 A fluindo para cima e o elemento z é uma fonte independente de corrente de 3   A fluindo para a esquerda. Selecionando uma árvore apropriada e usando os métodos da teoria dos gráficos, calcule i .

a) KVL:  - v g + i R ( t ) + L d i d t + 1 c ∫ - ∞ t   i d τ = 0

diferenciar e dividir por L

d 2 i d t 2 + 2 ( t ) L d i d t + 1 L d R ( t ) d t i + 1 L C i = 1 L d v g d t

d 2 i d t 2 + R ( t ) L d i d t + 1 L d R ( t ) d t + 1 L C i = 1 L k d v 2 d i t

Passo 2

b. Se in é a resposta natural, então

d 2 i n d t 2 + R ( t ) L - d i n d t + 1 L d R ( t ) d t + 1 L C i n = 0 (i)

Se i/f é a resposta forçada, então

d 2 i f d t 2 + R ( t ) L d i f d t + 1 L d R ( t ) d t + 1 L C i f = 1 L d v g d t (ii)

Adicionando (i) e (ii) temos

d 2 c n + L f d t 2 + R ( t ) L d i n + L f d t + 1 L d R ( t ) d t + 1 L C l n + l f

= 1 L d v g d t

Resposta

= 1 L d v g d t

Exercícios de Livros Relacionados

31-Mostre que, quando as equações 4.16, 4.17 e 4.19 são resolvidas para iB, o resultado é idêntico à Equação 2.25.
30-Use o método das tensões de nó para determinar a potência fornecida pela fonte de tensão de 20 V no circuito da Figura P4.30. Figura P4.30
29-Suponha que você seja um engenheiro projetista e alguém de sua equipe seja designado para analisar o circuito mostrado na Figura P4.29. O nó de referência e a numeração dos nós mostrados na figura
A fonte variável de corrente cc no circuito da Figura P4.57 é ajustada de modo que a potência gerada pela fonte de corrente de 40 mA seja igual a zero. Determine o valor de i c c .a) Você usaria o mét
a) Você usaria o método das tensões de nó ou das correntes de malha para determinar a potência absorvida pela fonte de 20 V no circuito da Figura P4.56? Explique sua escolha.b) Use o método que você s