Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 4.Problemas - Ex. 23

23-

Use o método das tensões de nó para determinar o valor de vo no circuito da Figura P4.23.

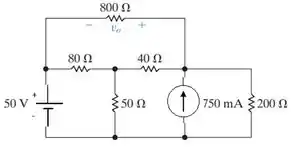
Figura P4.23

Passo 1

Falaaa bb, vamos fazer mais uma questãozinha?!

Então, usando o método das tensões de nó, temos:

v 1   -   50 80   + v 1 50   + v 1   -   v 2 40   =   0    

v 2   -   v 1 40   -   0.75   + v 2 200   + v 2   -   50 800   =   0

Passo 2

Passando essas equações para a forma padrão:

v 1 1 80   + 1 50 + 1 40 +   v 2   - 1 40 = 50 80  

v 1   ( - 1 40 )   +   v 2   ( 1 40 + 1 200   + 1 800   ) =   0.75   + 50 800  

Ao resolvermos, a gente chega em:

v1 = 34 V;

v2 = 53.2 V.

Logo,

vo = v2 − 50 = 53.2 − 50 = 3.2 V.

Passo 3

Verificando cada componente, temos:

ig = 50   -   34 80   + 50   -   53.2 800   =   196   m A  

p50V = - 50 * ( 0.196 )   =   - 9.8 W

p80Ω = 50   -   34 2 80   =   3.2 W  

p800Ω = 50   -   53.2 2 800   =   12.8   m W

p40Ω = 53.2   -   34 2 40   =   9.216 W

p50Ω = 342 50   =   23.12 W  

p200Ω = 53.2 2 200   = 14.1512W

p0.75A = - ( 53.2 ) * ( 0.75 )   =   - 39.9 W

∑pconsumida = 3.2 + .0128 + 9.216 + 23.12 + 14.1512 = 49.7W

∑pfornecida = 9.8 + 39.9 = 49.7 (Verificado)

Resposta

vo = 3.2 V.

Exercícios de Livros Relacionados

Mostre que o gráfico e planar.
Se um elemento 6 e adicionado em paralelo com o elemento 5 no Ex. 6.2.2, calcule todas as arvores do gráfico resultante.
Calcule o número de ramos de arvores e de enlaces no gráfico da Fig. 6.2.
Calcule todas as arvores do gráfico mostrado.
Na Figura do Ex. 6.2.2, considere i 2 e i 4 como sendo correntes de enlace nos elementos 2 e 4, fluindo para a direita. Considere i 1 , i 3 e i 5 como três correntes que descem. Calcule as três corren