Enunciado
Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 4.Problemas - Ex. 50
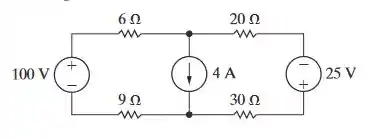
a) Suponha que a tensão da fonte de 100 V no circuito da Figura P4.49 seja alterada para 67,5 V. Determine a potência total dissipada no circuito.
b) Repita (a) com a fonte de corrente de 4 A substituída por um curto-circuito.
c) Explique por que as respostas para (a) e (b) são iguais.
d) Agora, suponhamos que você queira mudar o valor da fonte de 25 V, em vez da fonte de 100 V, no circuito na Figura P4.49, de modo a obter a mesma potência dissipada pela fonte de corrente determinada em (a) e (b). Use os resultados de (c) para calcular o novo valor dessa fonte de tensão.
Passo 1
Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!
A - Primeiramente, vamos definir os parâmetros de corrente para o circuito, com a alteração da fonte de tensão, para ficar mais fácil a visualização, vamos reescrever o circuito, com isso, nós temos que
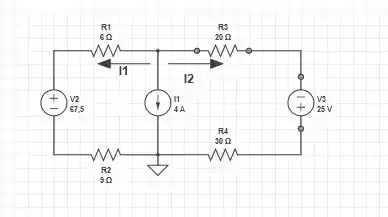
Usando a Lei de Kirchhoff das correntes, nós podemos caracterizar as relações das correntes no nó como
O que vamos fazer basicamente é um método dos nós, então precisamos saber quem é e , logo, pela Lei de Ohm, nós temos que
Juntando tudo, nós obtemos que
Resolvendo isso, nós temos que
Logo, temos que
A potência total dissipada no circuito é, uma vez que a fonte de tensão fornece potência à medida que a corrente sai dela e a fonte de corrente fornece 0 W. Então a potência dissipada é igual a
Passo 2
B - Quando é substituído por curto, usando a lei de tensão de Kirchhoff em torno da malha esquerda (a direção de é tomada oposta aqui, em oposição à primeira figura para simplificar).
De forma similar, . A corrente de curto-circuito é igual a
Assim, as respostas permanecerão inalteradas, uma vez que a fonte de tensão fornece energia e a fonte de corrente tem tensão zero através dela (portanto, tem n potência associada a ela) e as correntes permanecem as mesmas. Assim, a potência dissipada permanece a mesma que em (a)
C - Da parte (a) e (b) podemos deduzir que em ambos os casos, a tensão na fonte de corrente é 0 V e a corrente através dela é 4 A e o resto do circuito permanece o mesmo. Assim as respostas são as mesmas.
Passo 3
D – O circuito fica desse jeito
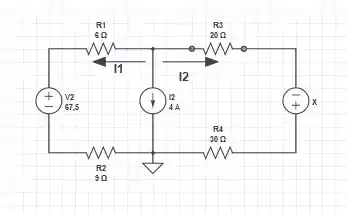
Para a mesma potência dissipada descrita nos circuitos acima, isto é, , logo, . Aplicando a LKT nós temos
Isto nos fornece...
Logo
Para o loop 2, nós vamos aplicar novamente LKT
Colocando nós temos que é igual a
Logo, o valor da fonte de tensão é .