Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 3.Problemas - Ex. 61

Use uma transformação Y-D para determinar (a) i o; (b) i 1; (c) i 2 e (d) a potência fornecida pela fonte ideal de corrente do circuito da Figura P3.61.

Passo 1

Primeiro iremos realizar a transformação delta/estrela

R 1 = 320 ∙ 20 320 + 20 + 50

R 1 = 16.4   Ω

R 2 = 320 ∙ 50 320 + 20 + 50

R 3 = 20 ∙ 50 320 + 20 + 50

R 3 = 2.6   Ω

R 2 + 600 | | R 3 + 100 + R 1

( 41   + 600 ) | | ( 2.6   + 100 )   +   16.4

R e q = 641 ∙ 102.6 641 + 102.6 + 16.4 = 104.8   Ω

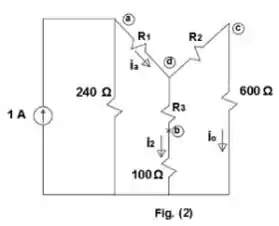
Passo 2

Utilizando de um divisor de corrente

i a = 240 240 + 104.8 1

i a = 0.7 A

i b = 104.8 240 + 104.8 1

i b = 0.3 A

Na figura (2) usando novamente divisor de corrente

i 2 = i a R 2 + 600 R 2 + 600 + R 3 + 100

i 2 = 0.7 41 + 600 41 + 600 + 2.6 + 100

i 2 = 0.6 A

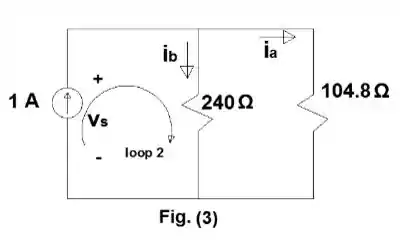
Agora equacionando o nó d:

i a - i 2 - i 1 = 0

i o = i a - i 2

i o = 0.7 - 0.6

i o = 0.1 A

Passo 3

Da figura (1), e aplicando a Lei de Kirchhof no Loop 1:

- i b 240 + i 1 320 + i o 600 = 0

- 0.3 ∙ 240 + 320 i 1 + 0.1 ∙ 600 = 0

320 i 1 = 12

i 1 = 37.5 m A

Na figura (3) utilizando a Lei de Kirchhof no Loop 2:

- v s + 240 i b = 0

- v s + 240 ∙ 0.3 = 0

v s = 72 V

P = v s i s

= 72   ∙ 1  

  =   72   W

Resposta

  1. 0.1 A
  2. 37.5 mA
  3. 0.6 A
  4. 72 W

Exercícios de Livros Relacionados

51. Determine a resistência equivalente nos terminais a - b para cada um dos circuitos mostrados na figura a seguir.
Determine a resistência equivalente Rab para cada um dos circuitos da Figura P3.8
Para cada um dos circuitos mostrados naFigura P3.3, a) identifique os resistores ligados em série,b) simplifique o circuito substituindo os resistores ligados em série por resistoresequivalentes
Para cada um dos circuitos mostrados naFigura P3.4,a) identifique os resistores ligados em paralelo,b) simplifique o circuito substituindo os resistores ligados em paralelo por resistores equivalentes
a) Determine a potência dissipada em cada resistor do circuito da figura 3.9b) Determine a potência fornecida pela fonte de 120 V.c) Mostre que a potência fornecida é igual à potência dissipada.