Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 2.Problemas - Ex. 51
51. Determine a resistência equivalente nos terminais para cada um dos circuitos mostrados na figura a seguir.
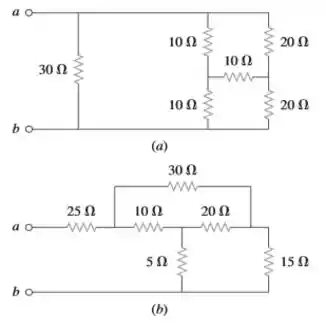
Passo 1
a) Olha só! Vamos destacar os nós importantes desse primeiro circuito com pontinhos coloridos. Pontos da mesma cor, indicam a mesma .
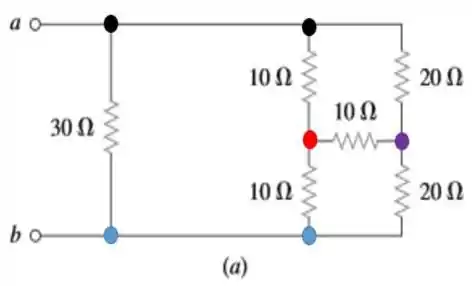
Os três resistores de formam uma conexão estrela. Como esse tipo de conexão não é a ideal para trabalharmos nesse caso, bora utilizar a conversão estrela-triângulo, ou também chamada de .
Onde ...
Desse modo utilizando as fórmulas da transformação abaixo, que já conhecemos:
Obtemos que...
Passo 2
E o nosso circuito fica assim:
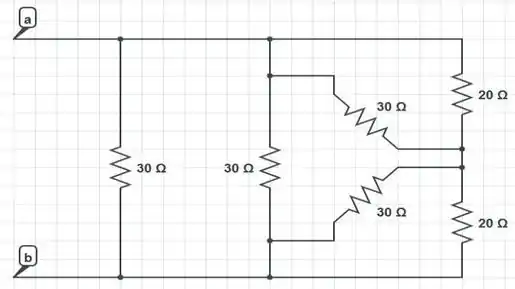
Dessa figura, podemos tirar algumas coisas interessantes:
E com isso, fazendo os cálculos necessários...
E depois...
Obtemos a seguinte aparência final para o nosso circuito:
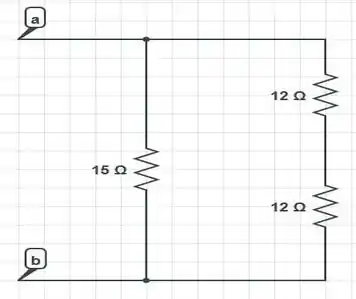
Onde desse modo, vemos que a resistência equivalente é dada por:
Passo 3
b) Para esse caso, vamos seguir os mesmos passos da letra anterior. Primeiro, destacar os nós desse circuito.
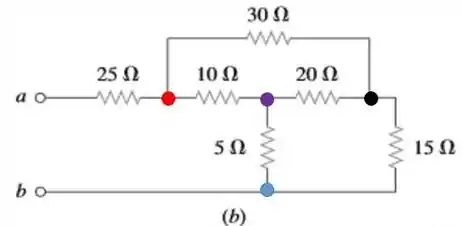
Os resistores de e formam uma conexão estrela. Como esse tipo de conexão, assim como na letra anterior, não é a ideal para trabalhar, bora utilizar a conversão estrela-triângulo.
Onde , e ... Desse modo utilizando as fórmulas da transformação abaixo:
Obtemos que...
Passo 4
E o nosso circuito fica assim:
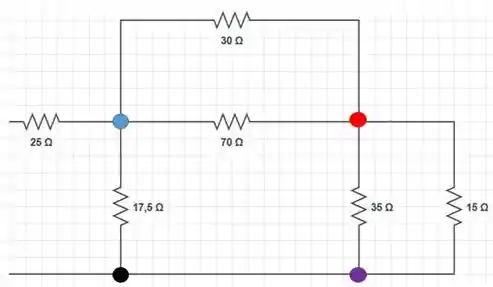
Dessa figura, podemos tirar algumas coisas interessantes:
E com isso, fazendo os cálculos necessários...
E vemos então, que a resistência equivalente , é dada por: