Ensaios em transformadores
Teoria
Fala aí, pessoal, hoje nos vamos conversar sobre os dois tipos de ensaio que fazemos para determinar os parâmetros que vemos num circuito de transformador que está bem aqui embaixo:
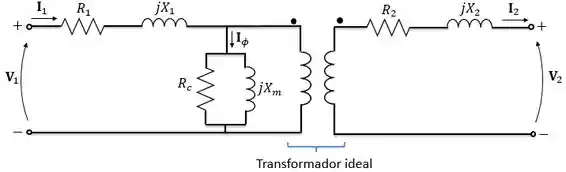
Onde:
Não se preocupem com o que fazer com e , agora é a hora de calcular e mais pra frente vamos ver como aplicar eles nos nossos circuitos.
Ensaio de Curto-Circuito
Esse ensaio é utilizado para determinar a impedância equivalente série . Que é igual a soma da impedância do lado primário com a impedância do secundário refletida ao primário:
Então nós curto-circuitamos o secundário do transformador e aplicamos tensão nos terminais do primário. Geralmente nesse ensaio utilizamos o primário como o lado de alta do transformador.
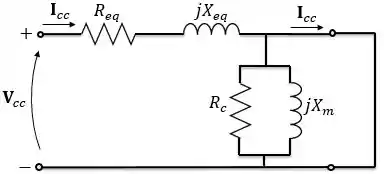
Quando curto-circuitamos o secundário, fazemos com que toda a corrente circule pelo curto e que a corrente do ramo de excitação seja zero. Então, podemos considerar que a impedância do ensaio de curto-circuito vista pelo primário é:
Com os instrumentos de medidas necessários, a gente mede, em módulo e valor eficaz, a tensão aplicada , a corrente de curto-circuito e a potência . A partir delas, podemos determinar a resistência e reatância equivalentes referidas ao primário através das fórmulas abaixo:
Caso seja necessário obter o circuito equivalente , podemos fazer a seguinte aproximação:
Vamos fazer um exemplo numérico para você ver como funciona!
As medidas obtidas em um ensaio de curto-circuito com um transformador de e foram e . Determine a resistência equivalente e a reatância equivalente série referidas ao lado de alta do transformador.
Passo 1:
De acordo com as medidas fornecidas pelo enunciado, temos:
Passo 2:
Então, aplicando as fórmulas:
Lembrando que esses parâmetros são referentes ao lado de alta do transformador!
Ensaio de Circuito Aberto
O ensaio de circuito aberto ou a vazio é feito com o secundário em aberto e aplicando a tensão nominal no primário. Normalmente, o lado de baixa tensão é utilizado como primário nesse ensaio. Então, vamos considerar o seguinte modelo referido ao primário:
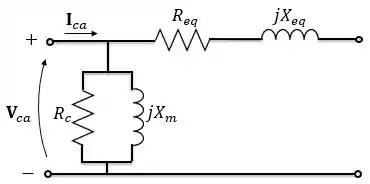
Esse ensaio é utilizado para determinar a reatância e resistência do ramo de excitação ( em paralelo com ) também pode ser usado para obter as perdas que ocorrem no núcleo do transformador.
Nesse circuito, a impedância equivalente do ensaio em circuito aberto é a própria impedância de excitação:
Nesse ensaio também medimos, em módulo e valor eficaz, a tensão , a corrente e a potência . Com essas medidas calculamos os parâmetros do ramo de excitação através das fórmulas abaixo:
Utilize apenas essas fórmulas para o ensaio de circuito aberto! Existem outras fórmulas que a gente conhece que relacionam corrente, tensão, potência e impedância, mas apenas essas funcionam para o ramo de excitação, já que o ramo é formado por dois elementos em paralelo.
Vamos continuar aquele exemplo anterior.
Agora foi feito um ensaio de circuito aberto no mesmo transformador e , com o lado de baixa energizado e as medidas obtidas foram e . Determine os parâmetros do ramo de excitação e as perdas no núcleo desse transformador.
Passo 1:
De acordo com as medidas fornecidas pelo enunciado, temos:
As perdas no núcleo são exatamente iguais à medida obtida para a potência no ensaio a vazio, ou seja:
Logo, se tivéssemos que calcular o rendimento, teríamos uma nova parcela para adicionar as perdas do transformador.
Passo 2:
Aplicando as fórmulas:
Lembrando que esses parâmetros são referentes ao lado de baixa do transformador!
Agora é praticar!
Ensaio de Circuito Aberto
Exercícios Resolvidos
Exercício Resolvido #1
Livro Fitzgerald – p.114 – Problema 2.8
O fabricante calcula que o transformador do problema anterior tenha uma indutância de dispersão de secundário igual a .
Calcule a indutância de magnetização quando referida ao secundário.
Uma tensão de e é aplicada ao secundário. Calcule a tensão resultante de circuito aberto do primário e a corrente de secundário que resultaria se o primário fosse curto circuitado.
Enunciado problema anterior: Um transformador monofásico de tem uma tensão nominal de placa de a qual se baseia na relação de espiras de seus enrolamentos. O fabricante calcula que a indutância de dispersão do primário seja e a indutância de magnetização do primário seja .
Passo 1
A indutância de magnetização referia ao primário é . Como
Temos que a indutância de magnetização referida ao secundário será:
Passo 2
Vamos desenhar o modelo desse transformador referido para o secundário. Mas antes, temos que encontrar as reatâncias:
Refletindo para o secundário:
Passo 3
Então, quando uma tensão de é aplicada no secundário e o primário está aberto, temos o seguinte modelo referido ao secundário.
Então, utilizando divisor de tensão, a tensão resultante de circuito aberto do primário refletida para o secundário, será:
Agora temos que usar a relação de transformação para encontrar a tensão de circuito aberto no primário.
Passo 4
Agora, temos que calcular a corrente do secundário quando o primário está curto circuitado. Então, temos o circuito abaixo:
Primeiro vamos calcular a reatância equivalente do circuito:
Logo, a corrente no secundário será:
Resposta
Exercício Resolvido #2
Livro Fitzgerald – p.114 – Problema 2.9
Um transformador de e tem uma reatância de magnetização (quando medida nos terminais de ) de . O enrolamento de tem uma reatância de dispersão de , e o enrolamento de tem uma reatância de dispersão de .
Com o secundário em aberto e aplicados ao enrolamento do primário , calcule a corrente de primário e a tensão de secundário.
Com o secundário curto-circuitado, calcule a tensão de primário da qual resulta a corrente nominal no enrolamento do primário. Calcule a corrente correspondente no enrolamento do primário.
Passo 1
De acordo com enunciado, podemos desenhar o seguinte modelo para esse transformador:
Como nada foi dito sobre as resistências desse transformador, vamos desconsiderá-las.
Passo 2
Para a letra , vamos aplicar no primário e deixar o secundário aberto. Para facilitar o cálculo, vamos usar o modelo referido ao primário do transformador.
Refletindo a reatância do secundário para o primário, temos:
Então, agora que todas as impedâncias estão referidas ao primário, vamos desenhar o modelo :
Como o secundário está aberto, a corrente circula apenas pelo primário. Logo, a corrente do primário será:
Passo 3
Já a tensão do secundário refletida é aquela aplicada na reatância de magnetização. Então, aplicando divisor de tensão:
Agora temos que usar a relação de transformação para encontrar a tensão de circuito aberto no secundário.
Passo 4
Na letra , o secundário é curto circuitado:
Temos que calcular que resulta com seu valor nominal. O valor nominal de é calculado utilizando os valores de potência aparente e tensão nominal do primário.
Aplicando a lei das tensões de Kirchhoff na malha da esquerda:
Passo 5
Para encontrarmos , temos que determinar antes. Usando divisor de corrente:
Calculando a tensão do primário:
Resposta
Exercício Resolvido #3
Livro Fitzgerald – p.115 – Problema 2.17 (adaptado)
Os seguintes dados foram obtidos para um transformador de distribuição de e em um ensaio a :
Calcule o rendimento com a corrente de plena carga e a tensão nominal nos terminais, operando com um fator de potência de .
Passo 1
Como queremos encontrar apenas o rendimento, não precisamos considerar o modelo completo do transformador. Então, precisamos determinar a impedância equivalente série do transformador para utilizarmos o seu modelo série. Para isso, vamos utilizar as medidas obtidas no ensaio de curto-circuito.
Passo 2
Com os valores do ensaio em curto circuito, podemos calcular a impedância equivalente série , através das fórmulas:
Logo, a impedância equivalente série será:
Passo 3
O rendimento de um transformador é calculado pela seguinte fórmula:
Em que a potência de entrada é a soma da potência de saída somado com as perdas.
A potência de saída é a potência ativa na carga. Como o fator de potência é a potência ativa será.
Então, como a potência aparente nominal do transformador é .
Já as perdas estão relacionadas às perdas que ocorrem no enrolamento e no núcleo do transformador. Logo,
A perda no núcleo é a potência que medimos no ensaio de circuito aberto:
Passo 4
Já a perda nos enrolamentos pode ser calculada pela fórmula abaixo:
Então, precisamos encontrar a corrente do primário. Na letra , foi dito que a corrente é a de plena carga e atenção é nominal. Logo,
Agora podemos calcular a perda nos enrolamentos:
Passo 5
Como já calculamos a perda no núcleo e nos enrolamentos do transformador, vamos somá-las para encontrarmos as perdas totais nesse transformador.
Então, a potência de entrada será:
Logo, o rendimento do sistema será:
Resposta
Exercício Resolvido #4
Livro Fitzgerald – p.115 – Problema 2.15
A placa de um transformador monofásico de e indica que ele tem uma tensão nominal de . Um ensaio de circuito aberto é executado a partir do lado de baixa tensão, e as respectivas leituras nos instrumentos de medida são e . Do mesmo modo, um ensaio de curto-circuito, no lado de baixa tensão, fornece leituras de e .
Calcule a impedância equivalente em série, a resistência e a reatância do transformador referidas aos terminais de baixa tensão.
Calcule a impedância equivalente em série do transformador referida aos terminais de alta tensão.
Fazendo as aproximações apropriadas, desenhe um circuito equivalente para o transformador.
Determine o rendimento e a regulação de tensão se o transformador estiver operando na tensão e carga nominais (fator de potência unitário).
Repita a parte , supondo que a carga tenha um fator de potência de capacitivo.
Passo 1
De acordo com o enunciado, as medidas obtidas nos ensaios do transformador de e foram:
Circuito aberto (No lado de BT):
Curto circuito (No lado de BT):
Passo 2
Com os valores do ensaio em curto circuito, podemos calcular a impedância equivalente série:
Logo, a impedância equivalente série será:
Passo 3
A relação de transformação desse transformador pode ser calculada utilizando as tensões nominais do transformador:
Então, a impedância equivalente referida ao lado de alta (secundário) será:
Passo 4
Na letra , temos que desenhar um circuito equivalente para o transformador, como o abaixo:
Vamos desenhá-lo referente ao primário, já que todas as medidas feitas nos ensaios foram feitas pelo lado de baixa.
Fazendo a aproximação necessária, temos:
Passo 5
Para completarmos o modelo, ainda falta encontrarmos os valores dos parâmetros do ramo de excitação. Para isso, temos que usar as medidas obtidas no ensaio de circuito aberto e aplicar nas fórmulas:
Passo 6
Agora que temos os valores de todas as resistências e reatâncias, podemos desenhar o modelo abaixo:
Passo 7
A regulação de tensão é calculada pela seguinte fórmula:
Para o cálculo de regulação de tensão podemos desconsiderar os parâmetros transversais (ramo de excitação) e considerar o modelo série do transformador:
Já tínhamos calculado que:
Então, conectando a carga com fator de potência unitário, temos o circuito abaixo:
Na letra , o enunciado disse que o transformador está operando com seus valores nominais de tensão e corrente, ou seja, que a carga está sendo alimentada pelos valores nominais.
Então, vamos considerar que a tensão da carga está na referência, ou seja, seu ângulo é zero e como o valor nominal de tensão do primário é , temos:
Como o transformador alimenta uma carga com e com a corrente nominal, temos:
Logo,
Passo 8
Agora é aplicar a lei das tensões de Kirchhoff na malha do circuito:
Então, em nosso circuito, quando a carga está ligada, a tensão nos terminais do secundário é igual à tensão que está sendo aplicada na carga. Logo,
Agora, vamos analisar a condição sem carga. Quando não há carga conectada ao secundário, ou seja, quando o transformador está a vazio, temos o circuito abaixo:
Como o circuito está aberto, não tem circulação de corrente, logo não há queda de tensão nas impedâncias do circuito e toda a tensão aplicada pela fonte conectada no primário é aplicada nos terminais do secundário. Logo,
Então, a regulação de tensão desse sistema será:
Passo 9
O rendimento de um transformador é calculado pela seguinte fórmula:
Em que a potência de entrada é a soma da potência de saída somado com as perdas.
A potência de saída é a potência ativa na carga. Como o fator de potência é unitário a potência ativa é igual a potência aparente.
Então, como a potência aparente nominal do transformador é .
Já as perdas estão relacionadas às perdas que ocorrem no enrolamento e no núcleo do transformador. Logo,
A perda no núcleo é a potência que medimos no ensaio de circuito aberto:
Logo, as perdas totais são:
Então, a potência de entrada será:
Logo, o rendimento do sistema será:
Passo 10
Na letra , temos que fazer o mesmo que fizemos para letra , só que agora o fator de potência é capacitivo.
Então, vamos nessa!
Temos o mesmo circuito:
Mas como a carga agora temcapacitivo, o ângulo da corrente irá mudar. Já que
Como o fator de potência é capacitivo o ângulo do fator de potência é negativo, ou seja, . Logo, utilizando a fórmula da potência complexa:
Logo,
Uma outra maneira de se fazer é primeiro calcular o módulo da corrente:
Depois, sabendo que colocamos a tensão na referência e que quando o fator de potência é capacito a corrente está adiantada em relação à tensão, podemos concluir que seu ângulo é positivo.
Passo 11
Aplicando a lei das tensões de Kirchhoff na malha do circuito:
Então, em nosso circuito, quando a carga está ligada, a tensão nos terminais do secundário é igual à tensão que está sendo aplicada na carga. Logo,
Agora, vamos analisar a condição sem carga. Quando não há carga conectada ao secundário, ou seja, quando o transformador está a vazio, temos o circuito abaixo:
Como o circuito está aberto, não tem circulação de corrente, logo não há queda de tensão nas impedâncias do circuito e toda a tensão aplicada pela fonte conectada no primário é aplicada nos terminais do secundário. Logo,
Então, a regulação de tensão desse sistema será:
Passo 12
O rendimento de um transformador é calculado pela seguinte fórmula:
Em que a potência de entrada é a soma da potência de saída somado com as perdas.
A potência de saída é a potência ativa na carga. Como o fator de potência é a potência ativa será.
Então, como a potência aparente nominal do transformador é .
Já as perdas estão relacionadas às perdas que ocorrem no enrolamento e no núcleo do transformador. Logo,
A perda no núcleo é a potência que medimos no ensaio de circuito aberto:
Logo, as perdas totais são:
Então, a potência de entrada será:
Logo, o rendimento do sistema será:
Resposta
Exercício Resolvido #5
Livro Fitzgerald – p.115 – Problema 2.17 (adaptado)
Os seguintes dados foram obtidos para um transformador de distribuição de e em um ensaio a :
Calcule o rendimento com a corrente de plena carga e a tensão nominal nos terminais, operando com um fator de potência de .
Passo 1
Como queremos encontrar apenas o rendimento, não precisamos considerar o modelo completo do transformador. Então, precisamos determinar a impedância equivalente série do transformador para utilizarmos o seu modelo série. Para isso, vamos utilizar as medidas obtidas no ensaio de curto-circuito.
Passo 2
Com os valores do ensaio em curto circuito, podemos calcular a impedância equivalente série , através das fórmulas:
Logo, a impedância equivalente série será:
Passo 3
O rendimento de um transformador é calculado pela seguinte fórmula:
Em que a potência de entrada é a soma da potência de saída somado com as perdas.
A potência de saída é a potência ativa na carga. Como o fator de potência é a potência ativa será.
Então, como a potência aparente nominal do transformador é .
Já as perdas estão relacionadas às perdas que ocorrem no enrolamento e no núcleo do transformador. Logo,
A perda no núcleo é a potência que medimos no ensaio de circuito aberto:
Passo 4
Já a perda nos enrolamentos pode ser calculada pela fórmula abaixo:
Então, precisamos encontrar a corrente do primário. Na letra , foi dito que a corrente é a de plena carga e atenção é nominal. Logo,
Agora podemos calcular a perda nos enrolamentos:
Passo 5
Como já calculamos a perda no núcleo e nos enrolamentos do transformador, vamos somá-las para encontrarmos as perdas totais nesse transformador.
Então, a potência de entrada será:
Logo, o rendimento do sistema será:
Resposta
Exercício Resolvido #6
Livro Fitzgerald – p.117 – Problema 2.29 (adaptado)
Um transformador de potencial de e tem os seguintes parâmetros, vistos do enrolamento de alta tensão (primário):
Supondo que o secundário esteja em aberto e que o primário esteja conectado a uma fonte de , calcule o módulo e o ângulo de fase (em relação à fonte de alta tensão) da tensão nos terminais do secundário.
Calcule o módulo e o ângulo de fase da tensão do secundário se uma carga resistiva de for conectada aos terminais do secundário.
Repita a parte se a carga for trocada por uma reatância de .
Passo 1
Com os dados do enunciado, vamos desenhar o modelo desse transformador referido ao primário:
Passo 2
Na letra , uma fonte aplica uma tensão de no primário e o secundário está aberto.
Queremos encontrar o módulo e o ângulo da tensão no secundário, tomando a tensão no primário como referência, ou seja:
Como o secundário está aberto, não há circulação de corrente no secundário e a sua tensão é a aplicada na reatância de magnetização. Então, utilizando divisor de tensão:
Passo 3
Encontramos a tensão do secundário refletida para o primário, agora temos que usar a relação de transformação para encontrar a tensão no secundário.
Como
Temos:
Passo 4
Na letra , continuamos aplicando a mesma tensão no primário, mas conectamos uma resistência de , no secundário.
Como estamos trabalhando com o modelo referente ao primário, temos que refletir essa resistência para o primário:
Então, temos o seguinte circuito equivalente série referido ao primário.
Passo 5
Há várias formas de resolvermos esse circuito. Primeiro, vamos calcular a impedância equivalente do circuito.
Agora, vamos calcular a corrente
Passo 6
Aplicando divisor de corrente, podemos calcular a corrente que passa pela carga:
Encontramos a corrente do secundário refletida para o primário, agora temos que usar a relação de transformação para encontrar a corrente no secundário.
Como,
Logo,
Agora que temos a corrente que passa pela carga resistiva, vamos aplicar a lei de ohm e encontrar a tensão no secundário.
Passo 7
Na letra , o procedimento é exatamente igual, a única coisa que vai mudar é que agora a carga é uma reatância de .
Calculando a impedância equivalente do circuito:
Agora, vamos calcular a corrente
Passo 8
Aplicando divisor de corrente, podemos calcular a corrente que passa pela carga:
Encontramos a corrente do secundário refletida para o primário, agora temos que usar a relação de transformação para encontrar a corrente no secundário.
Como,
Logo,
Agora que temos a corrente que passa pela carga resistiva, vamos aplicar a lei de ohm e encontrar a tensão no secundário.
Resposta
Exercício Resolvido #7
Livro Fitzgerald – p.115 – Problema 2.15
A placa de um transformador monofásico de e indica que ele tem uma tensão nominal de . Um ensaio de circuito aberto é executado a partir do lado de baixa tensão, e as respectivas leituras nos instrumentos de medida são e . Do mesmo modo, um ensaio de curto-circuito, no lado de baixa tensão, fornece leituras de e .
Calcule a impedância equivalente em série, a resistência e a reatância do transformador referidas aos terminais de baixa tensão.
Calcule a impedância equivalente em série do transformador referida aos terminais de alta tensão.
Fazendo as aproximações apropriadas, desenhe um circuito equivalente para o transformador.
Determine o rendimento e a regulação de tensão se o transformador estiver operando na tensão e carga nominais (fator de potência unitário).
Repita a parte , supondo que a carga tenha um fator de potência de capacitivo.
Passo 1
De acordo com o enunciado, as medidas obtidas nos ensaios do transformador de e foram:
Circuito aberto (No lado de BT):
Curto circuito (No lado de BT):
Passo 2
Com os valores do ensaio em curto circuito, podemos calcular a impedância equivalente série:
Logo, a impedância equivalente série será:
Passo 3
A relação de transformação desse transformador pode ser calculada utilizando as tensões nominais do transformador:
Então, a impedância equivalente referida ao lado de alta (secundário) será:
Passo 4
Na letra , temos que desenhar um circuito equivalente para o transformador, como o abaixo:
Vamos desenhá-lo referente ao primário, já que todas as medidas feitas nos ensaios foram feitas pelo lado de baixa.
Fazendo a aproximação necessária, temos:
Passo 5
Para completarmos o modelo, ainda falta encontrarmos os valores dos parâmetros do ramo de excitação. Para isso, temos que usar as medidas obtidas no ensaio de circuito aberto e aplicar nas fórmulas:
Passo 6
Agora que temos os valores de todas as resistências e reatâncias, podemos desenhar o modelo abaixo:
Passo 7
A regulação de tensão é calculada pela seguinte fórmula:
Para o cálculo de regulação de tensão podemos desconsiderar os parâmetros transversais (ramo de excitação) e considerar o modelo série do transformador:
Já tínhamos calculado que:
Então, conectando a carga com fator de potência unitário, temos o circuito abaixo:
Na letra , o enunciado disse que o transformador está operando com seus valores nominais de tensão e corrente, ou seja, que a carga está sendo alimentada pelos valores nominais.
Então, vamos considerar que a tensão da carga está na referência, ou seja, seu ângulo é zero e como o valor nominal de tensão do primário é , temos:
Como o transformador alimenta uma carga com e com a corrente nominal, temos:
Logo,
Passo 8
Agora é aplicar a lei das tensões de Kirchhoff na malha do circuito:
Então, em nosso circuito, quando a carga está ligada, a tensão nos terminais do secundário é igual à tensão que está sendo aplicada na carga. Logo,
Agora, vamos analisar a condição sem carga. Quando não há carga conectada ao secundário, ou seja, quando o transformador está a vazio, temos o circuito abaixo:
Como o circuito está aberto, não tem circulação de corrente, logo não há queda de tensão nas impedâncias do circuito e toda a tensão aplicada pela fonte conectada no primário é aplicada nos terminais do secundário. Logo,
Então, a regulação de tensão desse sistema será:
Passo 9
O rendimento de um transformador é calculado pela seguinte fórmula:
Em que a potência de entrada é a soma da potência de saída somado com as perdas.
A potência de saída é a potência ativa na carga. Como o fator de potência é unitário a potência ativa é igual a potência aparente.
Então, como a potência aparente nominal do transformador é .
Já as perdas estão relacionadas às perdas que ocorrem no enrolamento e no núcleo do transformador. Logo,
A perda no núcleo é a potência que medimos no ensaio de circuito aberto:
Logo, as perdas totais são:
Então, a potência de entrada será:
Logo, o rendimento do sistema será:
Passo 10
Na letra , temos que fazer o mesmo que fizemos para letra , só que agora o fator de potência é capacitivo.
Então, vamos nessa!
Temos o mesmo circuito:
Mas como a carga agora temcapacitivo, o ângulo da corrente irá mudar. Já que
Como o fator de potência é capacitivo o ângulo do fator de potência é negativo, ou seja, . Logo, utilizando a fórmula da potência complexa:
Logo,
Uma outra maneira de se fazer é primeiro calcular o módulo da corrente:
Depois, sabendo que colocamos a tensão na referência e que quando o fator de potência é capacito a corrente está adiantada em relação à tensão, podemos concluir que seu ângulo é positivo.
Passo 11
Aplicando a lei das tensões de Kirchhoff na malha do circuito:
Então, em nosso circuito, quando a carga está ligada, a tensão nos terminais do secundário é igual à tensão que está sendo aplicada na carga. Logo,
Agora, vamos analisar a condição sem carga. Quando não há carga conectada ao secundário, ou seja, quando o transformador está a vazio, temos o circuito abaixo:
Como o circuito está aberto, não tem circulação de corrente, logo não há queda de tensão nas impedâncias do circuito e toda a tensão aplicada pela fonte conectada no primário é aplicada nos terminais do secundário. Logo,
Então, a regulação de tensão desse sistema será:
Passo 12
O rendimento de um transformador é calculado pela seguinte fórmula:
Em que a potência de entrada é a soma da potência de saída somado com as perdas.
A potência de saída é a potência ativa na carga. Como o fator de potência é a potência ativa será.
Então, como a potência aparente nominal do transformador é .
Já as perdas estão relacionadas às perdas que ocorrem no enrolamento e no núcleo do transformador. Logo,
A perda no núcleo é a potência que medimos no ensaio de circuito aberto:
Logo, as perdas totais são:
Então, a potência de entrada será:
Logo, o rendimento do sistema será:
Resposta
