Transformador Monofásico Completo
Produzido por Alexandre NunesTeoria
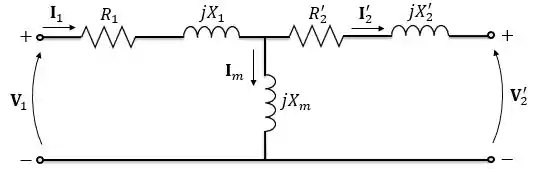
Até agora consideramos apenas os efeitos das resistências dos enrolamentos e do fluxo disperso. Com isso, tínhamos o modelo série abaixo:
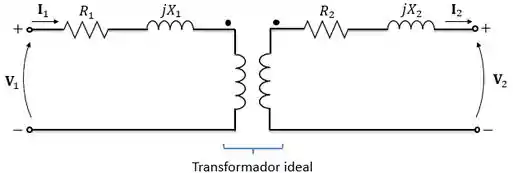
Agora, vamos aprender os modelos completos para transformadores. Nesses modelos, consideramos todas as perdas de um transformador.

Quando consideramos todas as perdas que ocorrem em um transformador, temos o modelo abaixo:

Adicionamos ao circuito série um braço de circuito com a resistência em paralelo com a reatância . Onde:
- Representa as perdas que ocorrem no núcleo do transformador.
- Reatância de magnetização que representa o fluxo mútuo resultante.
- Corrente de excitação do circuito.
Essa combinação em paralelo de e é chamada de ramo de excitação do circuito equivalente do transformador e chamamos sua impedância de .
Agora, vamos dar um zoom no ramo de excitação:
Podemos decompor a corrente de excitação em duas:
Onde é a componente de perdas no núcleo e é a componente de magnetização.
Modelo T de um transformador
Quando referimos todo o circuito de um transformador para o primário ou secundário, chamamos de circuito equivalente ou modelo . Por exemplo, dá uma olhada no circuito abaixo:
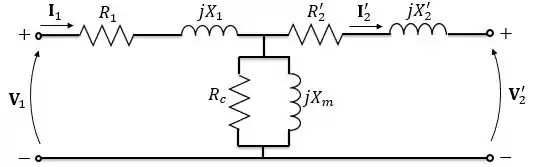
Esse é o modelo referido ao primário do transformador. A reflexão de grandezas é exatamente igual ao que fazíamos até aqui, ou seja:
Modelo L de um transformador
Muitas das vezes, para facilitar os cálculos, a gente desloca o ramo de excitação do meio do circuito para os terminais do primário ou secundário, como podemos ver nos circuitos referidos ao primário abaixo:

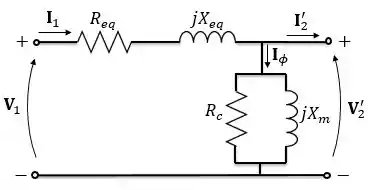
Onde:
Esses circuitos são chamados de modelo do transformador.
Podemos deslocar o ramo de excitação porque em transformadores a impedância desse ramo é muito alta, fazendo com que a corrente de excitação seja muito baixa e pouco colabore para as quedas de tensão nas impedâncias do enrolamento do primário ou secundário.
Agora que a gente já conhece todos os parâmetros que o transformador possui e já vimos como calcular cada parâmetro, bora fazer um exemplo com esses dados todos:
Exemplo
Considerando um transformador 220V:120V que tem os seguintes parâmetros vistos do enrolamento de alta tensão:
Calcule a tensão de secundário, caso o secundário esteja aberto e a tensão aplicada ao primário seja igual a 210V.
Passo 1:
Bom, galerinha, primeiro de tudo é desenhar esse circuito:

Nesse caso não precisamos colocar a resistência , pois ela é igual a zero.
Passo 2:
Nós podemos perceber que como não circula corrente pelo lado secundário, uma vez que ele está aberto, é igual à queda de tensão em cima do ramo de excitação:
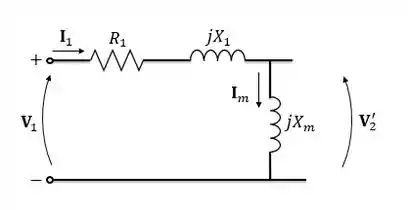
Passo 3:
Vamos aplicar os valores que já nos deram:
Passo 4:
Agora que encontramos a tensão do secundário referida ao primário, vamos refletir para o lado secundário através da relação de transformação, usando os valores nominais do transformador:
Como
Teremos:
Prontinho, a resposta já está completa. Agora é só praticar mais!
Modelo T de um transformador
Modelo L de um transformador
Exemplo
Passo 1:
Passo 2:
Passo 3:
Passo 4:
Exercícios Resolvidos
Exercício Resolvido #1
Livro Fitzgerald – p.113 – Problema 2.7
Um transformador monofásico de tem uma tensão nominal de placa de a qual se baseia na relação de espiras de seus enrolamentos. O fabricante calcula que a indutância de dispersão do primário seja e a indutância de magnetização do primário seja . Para uma tensão primária de a , calcule a respectiva tensão de secundário em circuito aberto.
Passo 1
Com os dados fornecidos elo enunciado vamos desenhar o modelo desse transformador referido para o primário. Mas antes, temos que encontrar as reatâncias:
Como nada foi dito sobre as resistências desse transformador, vamos desconsiderá-las. Logo, o circuito equivalente com o primário sendo alimentado por uma tensão de e o secundário em circuito aberto será:

Passo 2
Como o secundário está aberto, não tem corrente em seus enrolamentos e a tensão de seus terminais é a tensão aplicada na reatância de magnetização. Logo, aplicando divisor de tensão, temos:
Passo 3
Encontramos a tensão do secundário refletida para o primário, agora temos que usar a relação de transformação para encontrar a tensão no secundário.
Como
Temos:
Resposta
Exercício Resolvido #2
Livro Fitzgerald – p.118 – Problema 2.34
Um transformador monofásico de e tem impedâncias do primário e secundário de por unidade cada. A impedância de magnetização é por unidade. Todas as grandezas são por unidade na base do transformador. Calcule as resistências do primário e do secundário, além da indutância de magnetização (referidas ao lado de baixa tensão) em ohms e henrys.
Passo 1
Como estamos trabalhando com pu, temos que encontrar o valor base das grandezas. Como o enunciado disse que todas as grandezas estão na base do transformador, escolhemos seus valores nominais como base.
Escolhendo a potência do transformador como potência base:
Agora escolhemos um valor de tensão base para cada trecho do sistema, ou seja, para cada lado do transformador. Escolhendo as tensões nominais do transformador:
Passo 2
Com esses valores bases a gente já consegue determinar os valores base para as impedâncias do primário e secundário.
Passo 3
Agora, precisamos encontrar as impedâncias referidas para o primário e secundário em ohms. Para isso, temos que multiplicar o valor em pu pelo valor base:
A impedância do primário será:
Logo, a resistência e reatância do primário, em ohms, são:
Já a impedância do secundário será:
Logo, a resistência e reatância do secundário, em ohms, são:
Passo 4
Falta calcularmos a indutância de magnetização referida ao lado de baixa. Pelo enunciado, sabemos que:
Como queremos o valor referente ao primário, vamos multiplicar o valor em pu pela impedância de base do primário.
Como podemos ver, a impedância de magnetização é formada apenas pela reatância de magnetização, ela não possui a parcela resistiva.
Passo 5
Para finalizar, vamos calcular a indutância em henrys. Sabemos que
Logo,
Resposta
Exercício Resolvido #3
Livro Fitzgerald – p.117 – Problema 2.29 (adaptado)
Um transformador de potencial de e tem os seguintes parâmetros, vistos do enrolamento de alta tensão (primário):
Supondo que o secundário esteja em aberto e que o primário esteja conectado a uma fonte de , calcule o módulo e o ângulo de fase (em relação à fonte de alta tensão) da tensão nos terminais do secundário.
Calcule o módulo e o ângulo de fase da tensão do secundário se uma carga resistiva de for conectada aos terminais do secundário.
Repita a parte se a carga for trocada por uma reatância de .
Passo 1
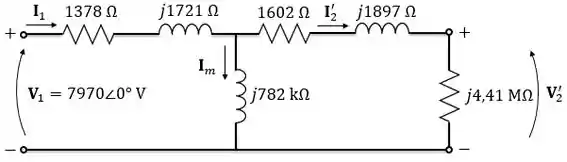
Com os dados do enunciado, vamos desenhar o modelo desse transformador referido ao primário:
Passo 2
Na letra , uma fonte aplica uma tensão de no primário e o secundário está aberto.

Queremos encontrar o módulo e o ângulo da tensão no secundário, tomando a tensão no primário como referência, ou seja:
Como o secundário está aberto, não há circulação de corrente no secundário e a sua tensão é a aplicada na reatância de magnetização. Então, utilizando divisor de tensão:
Passo 3
Encontramos a tensão do secundário refletida para o primário, agora temos que usar a relação de transformação para encontrar a tensão no secundário.
Como
Temos:
Passo 4
Na letra , continuamos aplicando a mesma tensão no primário, mas conectamos uma resistência de , no secundário.
Como estamos trabalhando com o modelo referente ao primário, temos que refletir essa resistência para o primário:
Então, temos o seguinte circuito equivalente série referido ao primário.

Passo 5
Há várias formas de resolvermos esse circuito. Primeiro, vamos calcular a impedância equivalente do circuito.
Agora, vamos calcular a corrente
Passo 6
Aplicando divisor de corrente, podemos calcular a corrente que passa pela carga:
Encontramos a corrente do secundário refletida para o primário, agora temos que usar a relação de transformação para encontrar a corrente no secundário.
Como,
Logo,
Agora que temos a corrente que passa pela carga resistiva, vamos aplicar a lei de ohm e encontrar a tensão no secundário.
Passo 7
Na letra , o procedimento é exatamente igual, a única coisa que vai mudar é que agora a carga é uma reatância de .
Calculando a impedância equivalente do circuito:
Agora, vamos calcular a corrente
Passo 8
Aplicando divisor de corrente, podemos calcular a corrente que passa pela carga:
Encontramos a corrente do secundário refletida para o primário, agora temos que usar a relação de transformação para encontrar a corrente no secundário.
Como,
Logo,
Agora que temos a corrente que passa pela carga resistiva, vamos aplicar a lei de ohm e encontrar a tensão no secundário.
