Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Transformadores Trifásicos

Ver Todos os Exercícios

Teoria

Fala aí! Hoje vamos trocar uma ideia sobre transformadores trifásicos. Bora lá entender um pouquinho sobre esses caras e como usá-los nos exercícios?

⭐ Veja também ⭐

O que é um transformador trifásico?

Como qualquer outro tipo de transformador, o transformador trifásico é um dispositivo usado para transformar energia elétrica de um circuito para outro, de modo a elevar ou abaixar a tensão conforme a necessidade.

O grande diferencial deste dispositivo é que ele possui três condutores elétricos de fase (daí o nome). Isso traz algumas vantagens em relação aos transformadores monofásicos ou bifásicos. Algumas delas tão listadas aqui:

👉 O maior número de fases proporciona maior eficiência na distribuição de energia.

👉 Requer menor quantidade de materiais de construção para entregar a mesma potência que um monofásico entregaria.

👉 Pode lidar com correntes maiores que um monofásico de mesmas proporções.

Bora então ver como esses caras são construídos pra proporcionar essas vantagens todas aí!

Tipos de ligação em transformadores trifásicos

A gente vai representar um transformador trifásico genérico desse jeito aqui:

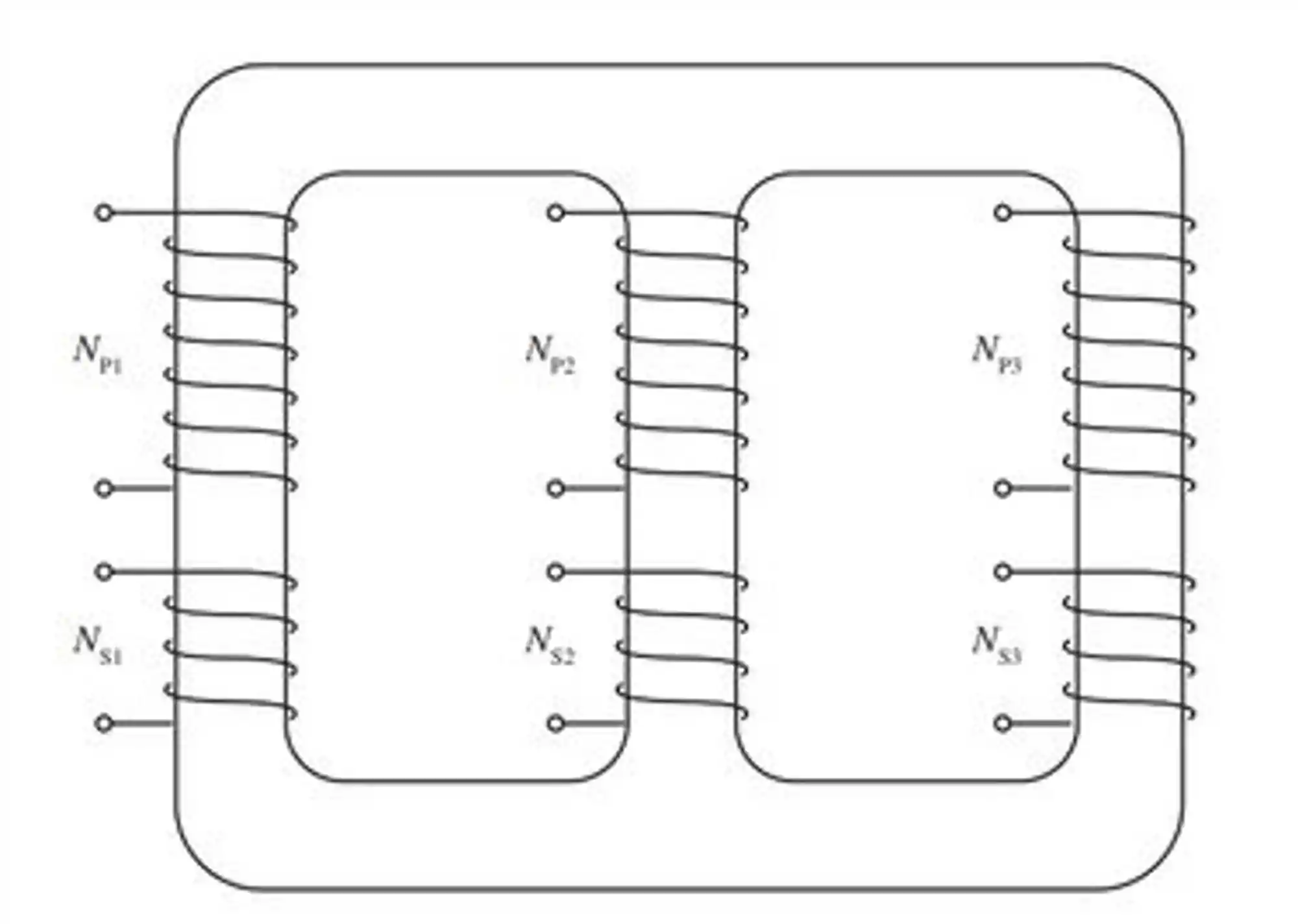
Representação de um transformador trifásico.
Representação de um transformador trifásico.

Esse é um transformador de um núcleo só, com três rolamentos primários ( ) e três rolamentos secundários ( ) .

Esses rolamentos podem ser conectados de dois modos diferentes: estrela (Y) ou delta (). Já vou te explicar o que cada um quer dizer 😉

Combinando as organizações para os primários e os secundários, são quatro possibilidades de ligação:

  1. Y-Y
  2. Y-
  3. -Y
  4. -

Esses modos vão proporcionar características diferentes. Então, bora ver cada uma delas mais detalhadamente.

Ligação Y-Y

Vamos representar dessa forma aqui:

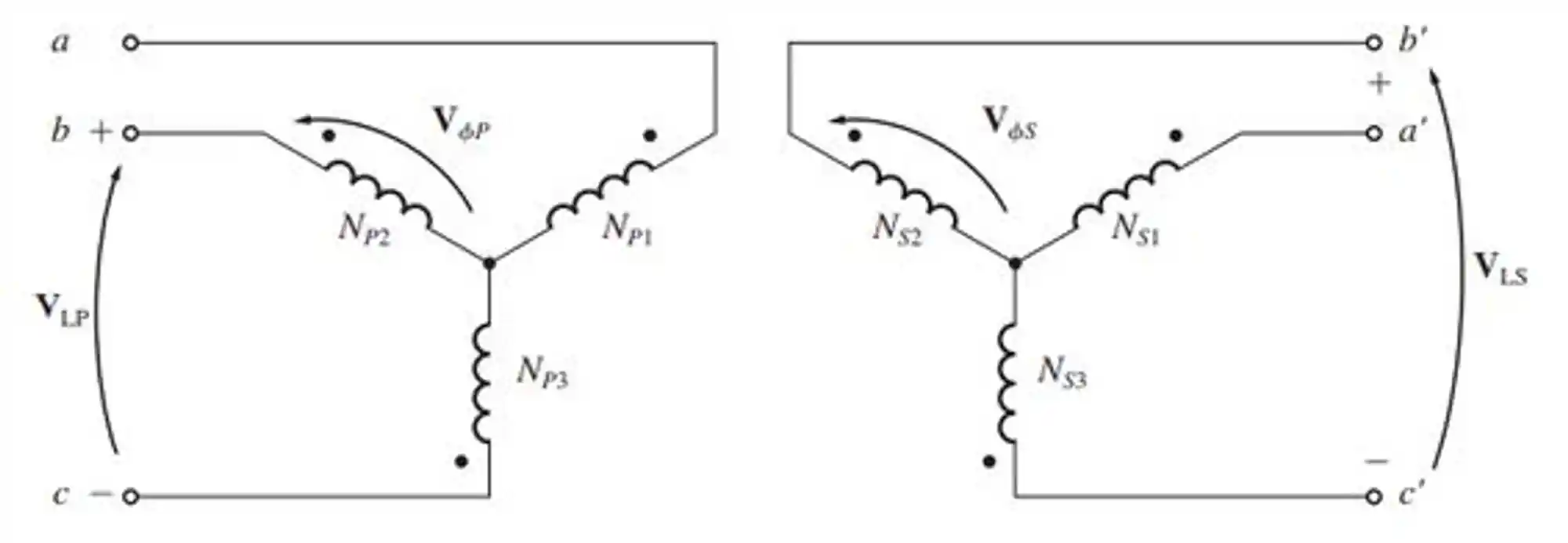
Ligação Y-Y.
Ligação Y-Y.

Consegue perceber que os rolamentos primários formam um tipo de Y, e o mesmo acontece com os secundários?

A relação entre a tensão de fase do lado primário e a tensão de fase do lado secundário é expressa assim:

E essa aqui é a relação entre a tensão de fase e tensão de linha, para a ligação Y:

Então, vamos escrever assim:

Ligação Y-

O primário continua ligado em Y, mas o secundário vai ficar ligado em :

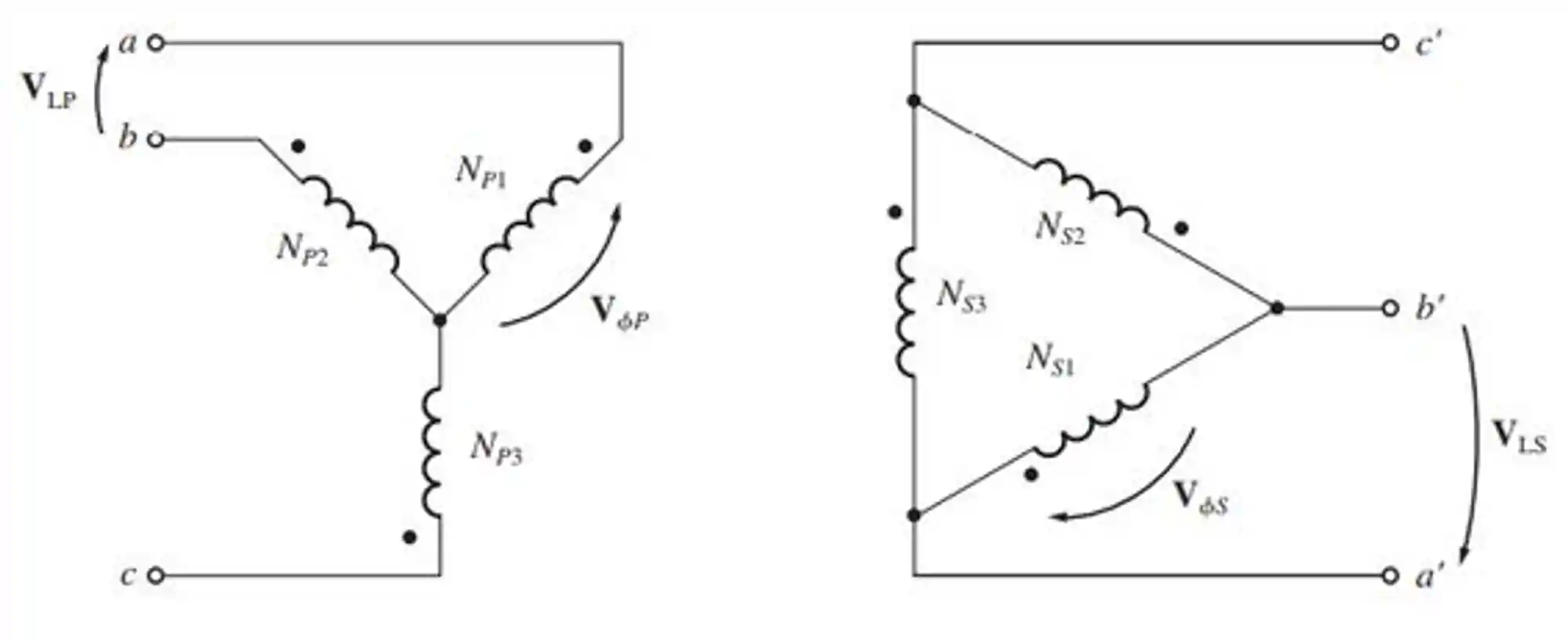
Ligação Y-
Ligação Y-

Aquela mesma relação ainda vale:

E a ligação Y continua tendo a relação:

Só que, pra ligação , as tensões de fase e de linha são iguais:

Então, dessa vez a gente tem o seguinte:

Ligação -Y

Agora temos o inverso do caso anterior:

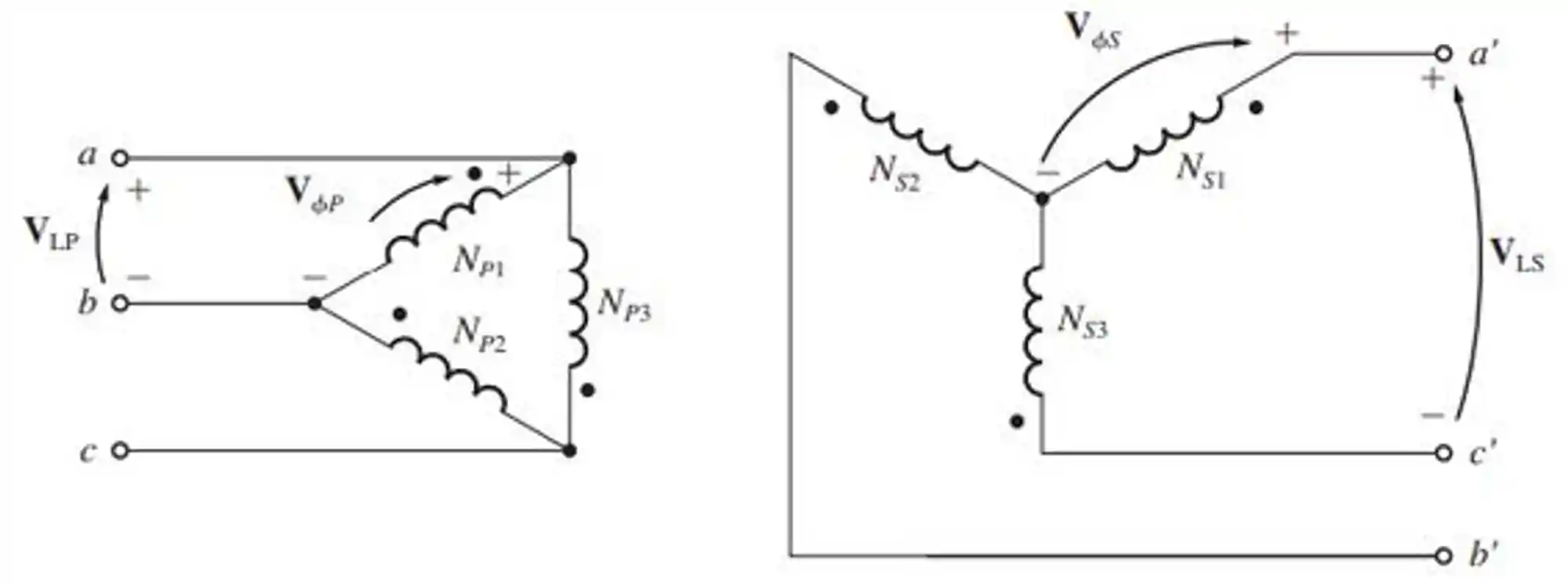
Ligação
Ligação

E aí é só inverter a relação que encontramos.

Ligação -

Agora, temos ambos os lados ligados em :

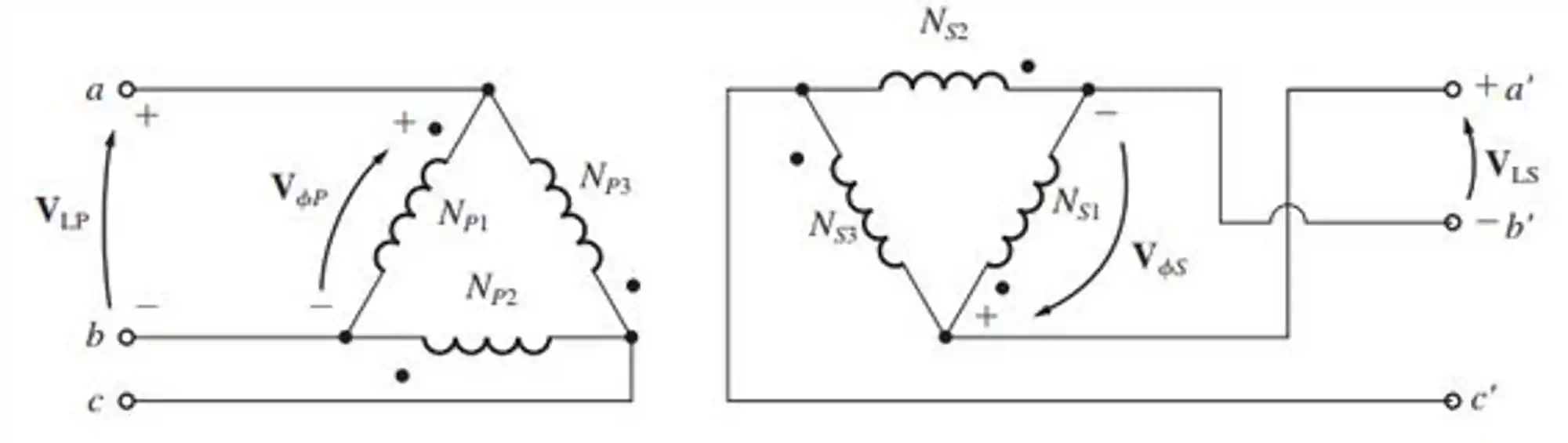
Ligação
Ligação

E as relações dessa vez são essas aqui:

E:

Então:

Sistema PU para transformador trifásico

O sistema por unidade fornece uma simplificação dos cálculos por meio de algumas relações que veremos logo em seguida.

A grande dica para resolver os problemas de transformadores trifásicos é analisar uma das fases tanto no caso de transformadores trifásicos quanto no caso dos bancos trifásicos, que é quando o transformador trifásico é composto por 3 transformadores monofásicos. Essa fase analisada vai se comportar exatamente igual aos monofásicos.

Se liga nessas relações que vamos usar para cálculos em PU:

  1. A potência de um dos transformadores monofásicos em VA em relação à potência total do transformador trifásico:

  1. A corrente de fase em A :

  1. A corrente de linha em A :

  1. A impedância de base em :

Belezinha? Bora ver em alguns exercícios resolvidos passo a passo como usar essas informações aí!

Ligação Y-

Ligação -Y

Ligação -

Sistema PU para transformador trifásico

Exercícios Resolvidos

Exercício Resolvido #1

Exercício 1 – Aula: Transformadores trifásicos – UNESP - Adaptada

Dispõe-se de uma rede elétrica trifásica 6,6kV e de três transformadores monofásicos 3800/220V. Desenhe um diagrama elétrico, indicando as ligações dos transformadores à rede elétrica e a três lâmpadas 200W/ 127V conectadas em Y. Obtenha as magnitudes magnitudes de todas as tensões e a relação de transformação. Indique estes valores no diagrama elétrico.

Passo 1

Vamos visualizar o que temos aqui:

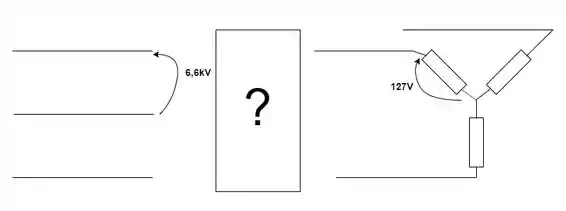
Passo 2

Tenho do lado primário enrolamentos que suportam 3800V e queremos ligar uma tensão de linha de 6,6kV, logo não podemos ligar em Δ, pois a a tensão de fase é igual a tensão de linha. Temos que ligar em Y, já que a tensão de linha do transformador será igual a

V L = 3800 *   3 = 6,6 k V

Passo 3

Agora para o secundário, sabemos que a carga está em Y e cada enrolamento dela precisa ser alimentado com 127V, logo a tensão de linha será igual a:

V L = 127 *   3 = 220 V

Que é igual a tensão de fase do secundário do transformador. O que podemos retirar disso? Que a tensão de fase tem que ser igual a tensão de linha do transformador, a ligação que obedece essa necessidade é a ligação Δ.

Passo 4

Vamos montar esse diagrama com as tensões:

Passo 5

Para finalizar, a relação de transformação do banco de transformadores é igual a relação entre a tensão de linha do lado primário e a tensão de linha do lado secundário:

a =   V L P V L S =   6600 V 220 V =   30

Resposta

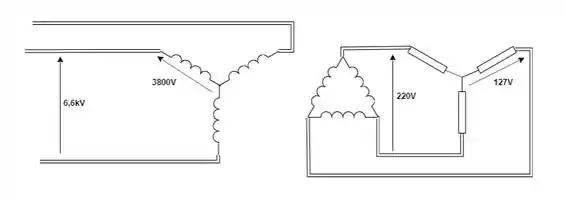
Exercício Resolvido #2

Exercício 4 – Aula: Transformadores trifásicos – UNESP – Adaptada

Uma carga composta de três resistores em Δ é conectada a um banco trifásico Δ – Y composto de três transformadores monofásicos que têm relação de espiras 5:1.

  1. Se a corrente na impedância da carga é de 8A, qual é o valor da corrente de linha do primário?
  2. Se a tensão de linha no primário é de 220V, qual é o valor da tensão na impedância da carga?

Passo 1

Se a corrente em cada fase da carga é igual a 8 A e a carga está em Δ, a corrente de linha que vem do lado secundário do transformador é igual a:

i L 2 = 8 *   3 = 13,86 A

Se nosso banco do lado secundário está conectado em Y, a corrente de linha é igual a corrente de fase. Logo a corrente que passa pelos enrolamentos do lado secundário é igual a 13,86 A .

Passo 2

Mas a questão me pede a corrente de linha do lado primário, então vamos utilizar a relação de espiras para a partir da corrente de secundário, achar a corrente nos enrolamentos do lado primário:

N 1 N 2 =   I 2 I 1

5 1 =   13,86 I 1

I 1 = 2,77 A

Passo 3

Essa corrente está passando no enrolamento do lado primário do transformador que está ligado em Δ, assim a corrente de linha é igual a :

I L 1 = 3 * 2,77 A = 4,8 A

Passo 4

Se a tensão de linha do lado primário é 220V e o primário está ligado em Δ, a tensão aplicada em seus enrolamentos é igual a tensão de linha 220V.

Pela relação de espiras novamente para achar a tensão nos enrolamentos do secundário:

N 1 N 2 =   V 1 V 2

5 1 =   220 V V 2

V 2 = 44 V

Passo 5

Como a tensão nos enrolamentos do lado secundário é igual a 44V e ele está ligado em Y, a tensão de linha é igual a:

V L 2 = 3 * 44 V = 76,2 V

Como a carga está ligada em Δ, a tensão de linha é igual a tensão de fase, logo a tensão de fase da carga é igual a 76,2V.

Resposta

  1. 4,8A
  2. 76,2V

Exercício Resolvido #3

Problema prático 2.12 – Máquinas elétricas - 6ª ed – Fitzgerald (pagina 97)

Uma carga trifásica é alimentada a partir de um transformador de 2,4kV: 460V e 150kVA cuja impedância equivalente em série é de 0,038 + j0,135 por unidade em sua própria base. Observa-se que a tensão de linha da carga é de 438V e está recebendo 96kW com um fator de potência unitário. Calcule a tensão no lado de alta do transformador. Faça os cálculos tomando como bases 460V e 100kVA.

Passo 1

Primeiro temos que calcular os valores de impedância de base para tanto a potência de 150kVA, quanto para 100kVA, pois faremos uma troca de base, uma vez que o problema me deu os dados na base de 150kVA, mas quer os cálculos na base de 100kVA.

Na base de 150kVA, a impedância base é igual a:

Z b a s e   t r a n s f o r m a d o r =   V 2 S =   460 2 150000 = 1,411 Ω

Na base de 100kVA, a impedância base é igual a:

Z b a s e   100 k V A =   V 2 S =   460 2 1 0 0000 = 2,116 Ω

Passo 2

Agora que já conhecemos os valores de impedância de base, vamos transformar os dados que temos de um para o outro. Para isso, vamos multiplicar a impedância equivalente série em pu por sua impedância base para chegar no valor dela em Ω:

0,038   +   j 0,135 p u * 1,411 Ω = 0,054 + j 0,190 Ω

Passo 3

Vamos dividir pela impedância base de 100kVA para obter o valor na nova base de potência:

( 0,054 + j 0,190 ) Ω 2,116 Ω = 0,025 + j 0,09   p u

Passo 4

Calculando a tensão na carga em pu, temos:

V c a r g a =   438 V 460 V = 0,952 ∠ 0 ˚   p u

Colocamos o ângulo igual a 0, pois ela erá nossa referência.

Passo 5

Calculando a potência em pu:

P c a r g a =   96 k W 100 k V A = 0,96   p u

Passo 6

Com os dados da potência e da tensão, podemos calcular a corrente requisitada pela carga:

I c a r g a =   0,96 0,952 = 1,01 ∠ 0 ˚   p u

O ângulo continua sendo igual a zero, pois o fator de potência é igual a 1.

Passo 7

A tensão no lado de alta é igual a:

V A = V c a r g a +   I c a r g a *   Z t r a n s f o r m a d o r

V A = 0,952 ∠ 0 ˚ +   1,01 ∠ 0 ˚ * ( 0,025 + j 0,09 )

V A = 0,952 ∠ 0 ˚ +   1,01 ∠ 0 ˚ * ( 0,093 ∠ 74,45 ˚ )

V A = 0,952 ∠ 0 ˚ +   0,094 ∠ 74,45 ˚

V A = 0,952 + 0,024 + j   0,091

V A = 0,977 + j   0,091

V A = 0,982 ∠ 5,32 ˚ p u

Passo 8

Esse valor está em pu, para calcular ele em Volts, devemos multiplicar pela tensão do lado de alta:

V A = 2400 * 0,982 ∠ 5,32 ˚ p u = 2357 V

Resposta

2357 V

Exercício Resolvido #4

Elaboração própria

Dois transformadores serão ligados em paralelo, porém descobrimos que enquanto o primeiro segue a sequência de fase positiva, o segundo transformador segue uma sequência de fase negativa. Ambas os transformadores tem amplitude de tensão igual a 20V. Se um aluno conectar um voltímetro entre as fases A dos dois transformadores, B dos dois transformadores e C dos dois transformadores, qual será o valor medido em cada um dos voltímetros.

Passo 1

O primeiro transformador segue uma sequência de fases positiva, logo podemos escrever as tensões como:

V A + = 20 ∠ 0 ˚ V

V B + = 20 ∠ - 12 0 ˚ V

V C + = 20 ∠ + 12 0 ˚ V

Passo 2

O segundo transformador segue uma sequência de fases negativa, logo podemos escrever as tensões como:

V A - = 20 ∠ 0 ˚ V

V B - = 20 ∠ + 120 ˚ V

V C - = 20 ∠ - 120 ˚ V

Passo 3

Assim podemos calcular a tensão que cada voltímetro fazendo a diferença de cada fase, para fase A:

V A + -   V A - =   20 ∠ 0 ˚ V -   20 ∠ 0 ˚ V = 0 V

V A + -   V A - =   0 V

Passo 4

Para fase B:

V B + -   V B - =   20 ∠ - 120 ˚ V -   20 ∠ + 120 ˚ V

V B + -   V B - = ( - 10 - j   17,32 ) V - ( - 10 + 17,32 ) V

V B + -   V B - = ( - 10 - j   17,32 + 10 - j 17,32 ) V

V B + -   V B - = ( - j   34,64 ) V

V B + -   V B - =   34,64   ∠ - 90 ˚   V

Passo 5

Para fase C:

V C + -   V C - =   20 ∠ + 120 ˚ V -   20 ∠ - 120 ˚ V

V C + -   V C - = ( - 10 + j   17,32 ) V - ( - 10 - J 17,32 ) V

V C + -   V C - = ( - 10 + j   17,32 + 10 + j 17,32 ) V

V C + -   V C - = ( j   34,64 ) V

V C + -   V C - =   34,64   ∠ + 90 ˚   V

Resposta

O voltímetro ligado entre as fases A:

0 V

O voltímetro ligado entre as fases A:

34,64   ∠ - 90 ˚   V

O voltímetro ligado entre as fases A:

34,64   ∠ + 90 ˚ V