Faça um programa para gerar os n primeiros termos da sequência:
Passo 1
E aí pessoal. Vamos resolver esse exercício!
Talvez a sequência do enunciado possa parecer um pouco aleatória. Mas na verdade é a famosa Sequência de Fibonacci, que é muito usada nos estudos de biologia e física.
Essa sequencia sempre começa com dois números pré-definidos, e daí pra frente os números seguintes é formado pela soma dos dois anteriores:
Para resolver essa sequência a gente pode utilizar um loop para calcular cada valor da sequência.
Se a gente vai usar um loop a gente vai precisar de pelo menos uma variável inteira para contar as iterações, vamos chamar de . Também vamos precisar receber do usuário a quantidade de iterações que ele deseja, então precisamos de uma variável inteira .
Mas aí tem um problema, se você ainda não sabe quantos termos vai ter a sequência de Fibonacci, então como você vai saber quantas variáveis vai precisar? Isso tem solução, acompanha comigo.
Para calcular um termo da sequencia você só precisa saber os dois termos anteriores. Então o que vamos fazer é, vamos calcular o termo da sequência, e imprimir o valor de na mesma hora. E antes de terminar a iteração a gente vai modificar o valor contido em e , para preparar para a próxima iteração:

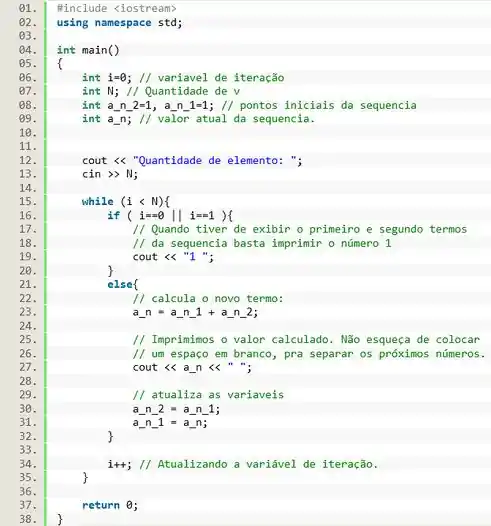
Vamos por a mão na massa. Pra começar vamos declarar as variáveis que vamos precisar.
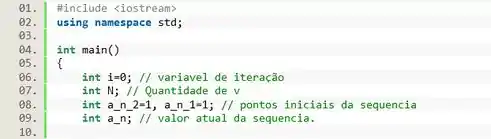
Inicializamos pois essa é a variável de iteração, e o primeiro termo da sequência ocorre quando . E as variáveis e são iniciadas desta forma pois representam os primeiros termos da sequência Fibonacci. E a variável será usada para calcular cada termo novo da sequência.
Passo 2
No passo seguinte, vamos usar o para pedir um número pro usuário, e com vamos armazenar o valor na variável

Passo 3
Show! Agora vamos pra parte massa da questão.
Primeiro de tudo, vamos iniciar o nosso loop. Ele vai durar enquanto a variável de iteração for menor que a quantidade de termos
![]()
A primeira coisa interessante pra notar é que no começo a nossa sequencia tem valores fixos. Quero dizer que, os dois primeiros termos da sequencia sempre são iguais a 1. Podemos usar uma estrutura para resolver isso:
- SE OU ENTÃO imprima 1.
- CASO CONTRÁRIO: calcule e imprima o próximo termo da sequencia
A primeira parte da condição fica assim. Note que devemos colocar um espaço em branco após o número. Isso vai evitar que o número seguinte fique colado no anterior.

Agora vamos considerar o caso em que precisaremos calcular a sequência. Abrimos dentro do comando adicionamos a expressão que calcula a sequência:
Em seguida a gente vai utilizar o comando para imprimir o conteúdo recém calculado.
E depois temos que atualizar as variáveis da sequência. Para calcular o próximo termo da sequência, o valor atual de passa para a variável , e o valor contido em passa para a variável Isso é necessário para preparar os as variáveis para a próxima iteração do laço!

E antes de concluir o loop a gente não pode esquecer de atualizar a variável de iteração :

E prontinho! Finalizamos mais uma questão.
Resposta