Parâmetros Adimensionais
Produzido por Giovanna RonzéTeoria
Vamos aumentar nossa gama de conhecimentos? Partiu!!
Bom, nesse momento ver quem são os parâmetros adimensionais que são mega importantes na convecção mássica… Já usamos cada um deles em diferentes situações da convecção mássica, mas agora vamos ver o que cada um deles nos indica… Vamos começar!
Número de Sherwood
Ele é o cara que qualifica a transferência de massa. É através dele que podemos ver a relação de existência da difusão ao mesmo tempo em que a convecção mássica, por meio da relação entre as resistências de cada uma… Vamos dar uma olhadinha nele:
Pra ficar mais claro que ele nos mostra a relação da difusão com a convecção, podemos escrevê-lo assim:
![]()
Essa é uma relação global, ou seja, ela é válida para em todos os pontos onde acontecem transporte de soluto.
Número de Schmidt
Ele representa a transferência da quantidade de movimento que acontece simultaneamente a transferência de massa… Olha a carinha dele aqui:
A relação feita por ele é em nível molecular, isso significa que os fenômenos são decorrentes das interações moleculares, sendo o correspondente ao momento e o correspondente a matéria.
Número de Stanton mássico
Ele nos mostra a relação entre a convecção mássica e a contribuição convectiva ao movimento do meio, ele é dado por:
A relação dele acontece em nível macroscópico, onde os parâmetros são analisados quantitativamente, para o momento teremos e para a matéria .
Número de Peclet mássico
Ele relaciona as resistências ao fenômeno da condução térmica e a influência do movimento do meio na transferência de calor convectiva, é dado por:
Ele apresenta uma relação em nível macroscópico, onde os parâmetros são analisados quantitativamente, para o momento teremos e uma parte em nível molecular, para a matéria .
Vamos agora montar uma tabelinha com as equações e quando são utilizadas pra gente não esquecer:
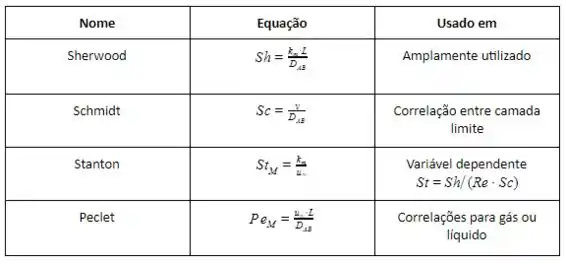
Agora vamos arrasar nos exercícios!
Número de Schmidt
Número de Stanton mássico
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria.
Dos parâmetros adimensionais para transferência de massa, separe-os em números primários, secundários e terciários.
Passo 1
Fala aí!! Vamos começar com as definições de número dimensional primário, secundário e terciário e por último a gente indica cada um dos parâmetros nessa classificação, ok?
Bom, o número adimensional primário é aquele que resulta da análise global de um fenômeno isolado, ou seja representa uma fração desse fenômeno, um instante… É normal ele apresentar um parâmetro cinemático.
O número adimensional secundário, surge da análise simultânea de dois fenômenos no mesmo nível de transferência… Já o número adimensional terciário, é aquele onde ocorre simultâneamente dois fenômenos em níveis diferentes de transferência, um macroscópico e o outro molecular.
Passo 2
Agora que temos as definições, vamos separar nossos parâmetros adimensionais, como número adimensional primário vamos ter o número de Reynolds e o número de Sherwood. Como parâmetro adimensional secundário temos o número de Schmidt e o número de Stanton e de parâmetro terciário temos o número de Peclet mássico.
Prontinho!
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #2
Elaboração própria.
Por meio da interpretação dos números adimensionais, construa um diagrama mnemônico para os parâmetros convectivos.
Passo 1
Eita! Diagrama mnemônico? Que isso minha gente?
Relaxa! Se liga só, é um quadro que sabendo montar direitinho ajuda e muito a gente pra lembrar de cada um dos nossos parâmetros adimensionais, vamos montando ele por partes!
Primeiro temos que desenhar um quadrado e em cada vértice vamos colocar algumas relações, olha só aqui:
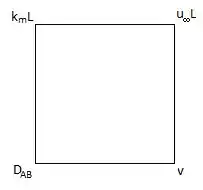
Passo 2
Agora vamos inserir setinhas, de forma que a ponta de cada seta indique a divisão da grandeza anterior pela que vem depois. Cada uma dessas setinhas será um número adimensional, olha como fica a carinha do diagrama mnemônico:
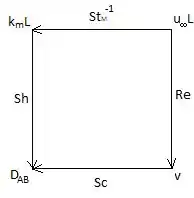
Opa! Mas peraí! O número de Peclet ficou de fora? Tá certo isso? Tá não! Lembra que ele é dado por:
Então ele é uma diagonal! Vamos colocar ele lá no nosso diagrama! Ficaremos com:
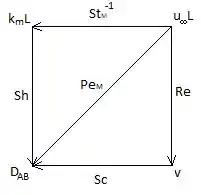
Show de bola! Montamos o diagrama mnemônico pedido!
Resposta
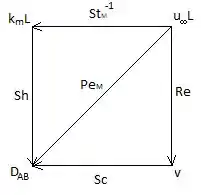
Exercício Resolvido #3
Adaptado de fundamentos da transferência de massa - Cremasco - 2ª Edição
Determine o valor de número de Schmidt do ar a 40°C e 1 atm.
Dado: , e
Passo 1
Vamos encontrar o número de Schmidt! Nossa equaçãozinha lá da teoria, diz que:
Não temos o , mas não podemos esquecer que ele é dado por:
Opa! Já que temos esses parâmetros, vamos achá-lo:
Precisamos ainda da difusão, que o enunciado nos deu parcialmente haha
Ainda temos uma continha pra resolver:
Beleza! Então o número de Schmidt será:
Prontinho! Encontramos ele!
Resposta
O número de Schmidt é:
Exercício Resolvido #4
Elaboração própria.
Encontre o valor de número de Sherwood para o escoamento de um fluido gasoso a 40°C e 1 atm, em torno de uma esfera.
Dado: e .
Passo 1
Para tudo! O número de Sherwood nós vimos como encontrar pela equação:
Mas nessa questão ele não nos dá nada do que temos aqui… E agora?
Agora a gente relaxa e respira fundo! É o seguinte, existem variações dessa correlação que aprendemos… Como estamos trabalhando nesse caso com um fluido gasoso passando por uma esfera, podemos usar essa relação aqui:
Mas vamos ficar atentos porque essa correlação só vale quando temos:
Como o número de Reynolds se enquadra nesse quesito, vamos usar essa relação aí!
Conseguimos!
Resposta
O número de Sherwood é:
Exercício Resolvido #5
Elaboração própria.
Dado o número de Sherwood como 9,84, o número de Reynolds como 1586 e o número de Schmidt como 0,6541. Encontre o valor do número de Stanton e o número de Peclet.
Passo 1
Fala aí! Tudo belezinha? Vamos encontrar o que esse enunciado tá pedindo! Ele quer o número de Stanton e o número de Peclet, eles podem ser obtidos pela relação que vimos antes, assim:
E os dados do nosso enunciado foram:
Não tá fazendo muito sentido, né? Esses dados não batem com o que precisamos para encontrar esses números adimensionais… Mas será que existe uma relação entre eles?

Existe sim! Vamos anotar elas aqui e não esquecer mais, ok?
O número de Stanton, pode ser encontrado usando:
Opa! Olha só isso! Temos tudinho! Então vamos calcular!
Passo 2
Agora vamos a relação do número de Peclet:
Substituindo nossos dados, ficamos com:
Opa! Mas e as unidades? Não esquece que são números adimensionais, beleza?
Show de bolinhas!
Resposta
Exercício Resolvido #6
USP - Lista de Química Geral I
O número de Stanton é um número adimensional que mede a relação entre o calor transferido a um fluido e seu calor específico, ele é muito usado em cálculos de fluxo de calor por convecção forçada em tubos. A expressão para o cálculo deste número é:
Em um determinado experimento, os seguintes valores foram determinados: coeficiente de transferência térmica, ; comprimento do tubo, ; calor específico do fluido, ; massa específica do fluido, ; velocidade de escoamento e o diâmetro do tubo,. Calcule o valor de Stanton para este experimento.
Passo 1
Olha só! Esse enunciado deu pra gente uma forma de encontrar o número de Stanton e pediu pra gente encontrar ele, belezinha?
Os dados foram os seguintes:
As unidades estão meio estranhas, né? Temos que ajustar isso aí!
Lembrando que o número de Stanton é adimensional, temos que ter as unidades do numerador igual a do denominador, certo?
Vamos então as conversões, primeiro com as mais conhecidas, sabendo que:
Agora vamos para as pouco conhecidas, esse aí é jarda, ok? E podemos converter ela para pés assim:
Além disso podemos usar as seguintes relações para conversão:
Passo 2
Usando essas relações aí, nossos dados vão ficar assim:
Agora vamos usar a equação com nossas unidades ajeitadinhas:
Resposta
Exercício Resolvido #7
Adaptado de UFS - Lista de exercícios de transferência de massa
Explique o significado físico dos números adimensionais de Reynolds, Sherwood, Stanton mássico e Schmidt e encontre uma única expressão que mostre como estes se relacionam matematicamente.
Passo 1
Bom, vamos começar explicando que os números adimensionais fazem relações entre parâmetros que nos ajudam a entender o acontecimento físico da transferência de massa. Dá só uma olhada no número de Sherwood, por exemplo, ele nos indica a relação entre o processo de difusão e o processo de convecção mássica, beleza?
Além disso o enunciado pede pra gente uma relação entre o número de Reynolds, Sherwood, Stanton mássico e Schmidt… Fomos apresentados para cada um deles na teoria separadamente, né?
Mas existem relações que são muito importantes da gente saber! Uma delas é exatamente a que relaciona esses quatro parâmetros adimensionais, e essa relação pode ser escrita assim:
Isso quer dizer que temos uma relação, onde é possível encontrar o número de Stanton mássico, a partir da divisão do número de Sherwood pela multiplicação do número de Reynolds com o número de Schmidt.
Belezinha!
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #8
Adaptado de USP - Processos de transferência de calor
Num processo farmacêutico, óleo de rícino (mamona) a 40°C escoa sobre uma placa aquecida muito larga de 6 m de comprimento, com velocidade de 0,06 m/s. Para uma temperatura de 90°C. Determine a força de atrito, por unidade de comprimento, sobre a placa.
Dados:
Passo 1
Essa questão aqui tá pedindo pra gente a força de atrito por comprimento da placa… Humm… Como vamos encontrá-la? Bom, podemos usar essa relação aqui, olha só:
Bom, precisamos então da tensão de cisalhamento, que pode ser encontrada usando a equação:
Parece que quanto mais a gente mexe mais complica, né? Relaxa! Só estamos levantando todos os parâmetros que vamos precisar para encontrar o que o enunciado tá pedindo pra gente. Vamos precisar do , para isso temos a relação:
Opa! Olha aí o número de Stanton! Precisamos dele! E uma das formas de encontrar ele é com a equação:
Agora que já selecionamos tudo! Vamos usar os dados do nosso enunciado para calcular todos esses caras aí e enfim encontrar a força de atrito por comprimento de placa!
Passo 2
Vamos começar calculando o número de Stanton:
Podemos então encontrar o :
A tensão de cisalhamento será:
E para fechar, a força de atrito será:
Prontinho! Conseguimos!