Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Transferência de massa entre fases

Ver Todos os Exercícios

Teoria

Fala aíííí! Até agora a gente tava vendo como se comporta a transferência de massa sempre entre fases iguais, né? No máximo, vimos a relação entre as duas fases, mas era apenas levando em conta um equilíbrio na interface…

Mas agora chegou aquele momento esperado por nós… Aprender como acontece a transferência de massa entre fases diferentes!!

Até por que é através desse estudo que vamos entender melhor como é feito o maior parceiro de um estudante… O café!

Sim, o café! No início temos duas fases o pó, em estado sólido, e a água, em estado líquido, para preparar ele vamos fazer o soluto ir de uma fase para a outra… Isso é exatamente o que acontece em uma transferência de massa entre fases!!

E porque é importante a gente aprender sobre isso? Bom, nessa parte aqui a gente vê diferentes técnicas que encontramos na indústria para separar um ou mais componentes de uma mistura que nos interesse, show de bola? Então vamos nessa!

A gente sabe que existe uma resistência a transferência de massa, isso quer dizer que tem uma dificuldade ao fluxo molar. Na convecção mássica, ela pode ser dada assim, olha só:

N A ,   Z = k m ⋅ C A - C A ∞

Esse N A ,   Z é o fluxo molar do soluto A na direção Z, o k m é o coeficiente convectivo de transferência de massa e esse C A - C A ∞ é a diferença de concentração. Dá uma olhada nessa figura aqui:

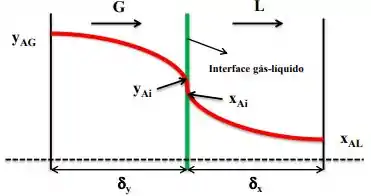
Aqui a gente tá visualizando dois filmes estagnados, tendo como espessuras δ y e δ x , e o soluto está indo da fase gasosa para a fase líquida, beleza? Nesse caso então, o fluxo global do soluto na fase gasosa será:

N A ,   Z = k y ⋅ y A G - y A i

A unidade do coeficiente de transferência de massa da fase gasosa ( k y ) fica desse jeito aqui:

k y = m o l s   d e   A á r e a ⋅ t e m p o ⋅ Δ y A

E a gente ainda pode colocar a equação do fluxo em função da pressão parcial, olha só:

N A ,   Z = k G ⋅ P A G - P A i

Podemos encontrar o coeficiente k G relacionando ele com o k y e a pressão total do sistema, assim:

k G = k y P

E a unidade dele fica:

k G = m o l s   d e   A á r e a ⋅ t e m p o ⋅ u n i d a d e   d e   p r e s s ã o

Mas a gente só viu o fluxo na fase gasosa, que é a mais leve, e na fase líquida, que é há mais pesada, como fica? Vamos ver:

N A ,   Z = k x ⋅ x A i - x A L

E o coeficiente de transferência de massa da fase líquida ( k x ) fica com suas unidades assim:

k x = m o l s   d e   A á r e a ⋅ t e m p o ⋅ Δ x A

E ele a gente pode representar como sendo uma função da concentração, desse jeitinho aqui:

N A ,   Z = k L ⋅ C A i - C A L

E o coeficiente k L a gente pode relacionar com o k x , a massa molecular e a densidade da parte líquida:

k L = k x ⋅ M L ρ L

E a unidade dele vai ser:

k L = m o l s   d e   A á r e a ⋅ t e m p o ⋅ u n i d a d e   d e   c o n c e n t r a ç ã o   m o l a r   d e   A

Os valores de y A i e de x A i podem ser determinados experimentalmente, podendo ser usada a lei de Henry que vai usar uma relação com a pressão parcial:

P A i = x A i ⋅ H

E usando a lei de Dalton, também fazendo uma relação com a pressão parcial, temos:

P A i = y A i ⋅ P

E sendo as pressões parciais as mesmas, vamos ficar com a relação que:

y A i = H P ⋅ x A i

Considerando m = H P , temos:

y A i = m ⋅ x A i

Teoria das duas resistências

Essa teoria foi proposta por Witman, ela considera que a absorção é governada somente pela difusão do soluto nas duas fases, ou seja, é possível estabelecer a continuidade do fluxo de A na fronteira entre as fases. Então temos que:

N A ,   Z = k y ⋅ y A G - y A i = k x ⋅ x A i - x A L

Ficamos com:

- k x k y = y A G   -   y A i x A L   -   x A i

Essa relação nos ajuda a determinar os coeficientes individuais da transferência de massa, basta a gente conhecer as composições do soluto na interface.

Coeficientes globais de transferência de massa

Esses coeficientes globais são alternativas que nos ajudam na determinação do fluxo de matéria, numa situação em que a resistência ao transporte de uma das fases em relação a outra seja desprezível. Nós ficaremos com:

N A ,   Z = K y ⋅ y A G - y A * e N A ,   Z = K x ⋅ x A * - x A L

Sendo esse K y e o K x os coeficientes globais de transferência de massa, na nossa situação das fases gasosa e líquida. E usando a mesma relação que já vimos ali em cima, vamos ter que a fração molar do soluto na fase A, no estado gasoso e líquido, terá a seguinte relação:

y A * = m ⋅ x A L e y A G = m ⋅ x A *

Relacionando então os coeficientes individuais com os globais, vamos ter, para a fase gasosa:

k y ⋅ y A G - y A i = K y ⋅ y A G - y A *

E ficaremos com:

k y K y = 1 / K y 1 / k y = y A G - y A * y A G - y A i = △ y A g l o b a l △ y A G

E no caso da fase líquida:

k x ⋅ x A i - x A L = K x ⋅ x A * - x A L

E temos que:

k x K x = 1 / K x 1 / k x = x A *   -   x A L x A i   -   x A L = △ x A g l o b a l △ x A L

Mas e se a gente tiver considerando que uma das resistências é desprezível? Bom, aí a gente pode dizer que:

1 K y = y A G   -   y A i N A ,   Z + y A i   -   y A * N A ,   Z

E substituindo as equações de equilíbrio na interface, onde y A * = m ⋅ x A L e y A i = m ⋅ x A i , vamos ter:

1 K y = y A G   -   y A i N A ,   Z + m ⋅ x A i   -   x A L N A ,   Z

Logo:

1 K y = 1 k y + m k x

E para o caso da fase líquido, seguindo o mesmo princípio, vamos ter:

1 K x = 1 m ⋅ k y + 1 k x

Ufaa! Agora que vimos tanta teoria tá na hora de praticar, né?

Teoria das duas resistências

Coeficientes globais de transferência de massa

Exercícios Resolvidos

Exercício Resolvido #1

Elaboração própria.

Defina os coeficientes k G e k L .

Passo 1

Fala aí! Vamos fazer essa definição que o enunciado está pedindo, ok?

Bom, k G é o coeficiente da fase gasosa que se relaciona com o k y e a pressão parcial do sistema, desse jeito aqui:

k G = k y P

E a unidade dele é:

k G = m o l s   d e   A á r e a ⋅ t e m p o ⋅ u n i d a d e   d e   p r e s s ã o

Já o k L é o coeficiente da fase líquida. Ele se relaciona com o k x , a massa molecular e a densidade da parte líquida do sistema, dessa forma:

k L = k x ⋅ M L ρ L

Sendo sua unidade dada por:

k L = m o l s   d e   A á r e a ⋅ t e m p o ⋅ u n i d a d e   d e   c o n c e n t r a ç ã o   m o l a r   d e   A

Prontinho!

Resposta

Passo 1.

Exercício Resolvido #2

Elaboração própria.

Explique a teoria das duas resistências.

Passo 1

Precisamos explicar a teoria, vamos lá!

A teoria das suas resistências foi proposta por Witman em 1923. Ela se baseava na absorção, sendo esta governada somente pela difusão do soluto nas duas fases, as quais foram supostas como filmes estagnados, ou seja, ela considera que o soluto deve vencer a resistência ao seu movimento em ambas as fases para que ocorra a separação. Sendo assim é possível estabelecer a continuidade do fluxo de A na fronteira entre as fases.

Através dela nós temos a relação:

- k x k y = y A G   -   y A i x A L   -   x A i

Ela é importante para determinação dos coeficientes individuais, k x e k y , envolvidos na operação de separação em um determinado ponto do equipamento de separação.

Prontinho!

Resposta

Passo 1.

Exercício Resolvido #3

Elaboração própria.

Quais os principais tipos de coluna de absorção utilizadas na indústria. Descreva o processo que ocorre em cada uma delas.

Passo 1

Vamos então listar e explicar os principais tipos de coluna de absorção!

Vamos começar com a câmara de pulverização, ela apresenta essa configuração:

Onde o líquido é pulverizado e remove o soluto do gás que flui pela parte de cima da câmara, além disso apresenta área superficial reduzida para absorção e necessita de elevada quantidade de água.

Temos também a coluna de pratos, que apresenta a seguinte configuração:

Nela o líquido desce em cascata por uma série de pratos onde entra em contato com o gás impuro, removendo o soluto dele. O gás limpo flui por cima da coluna.

E para finalizar, temos ainda, a coluna de enchimento, que tem sua configuração assim:

O líquido é pulverizado e remove o soluto do gás que flui no sentido de cima da câmara, ela usa uma quantidade reduzida de água e apresenta grande área superficial para absorção.

Finalizamos!

Resposta

Passo 1.

Exercício Resolvido #4

Universidade de Coimbra - Engenharia Química

Um tubo de borracha (neopreno vulcanizado), com 3,0 mm de diâmetro interno, 11 mm de diâmetro externo, e 1 m de comprimento é utilizado para transportar hidrogênio gasoso a 2 atm e 27 ° C .

  1. Calcule a perda de hidrogénio através da parede de borracha, em mol/h.
  2. Discuta como varia essa perda com as condições de pressão e temperatura do hidrogênio.

Dado: A solubilidade do hidrogênio na borracha S = 2,28 ⋅ P   m o l   H 2 / m 3 , sendo P a pressão, e a difusividade do hidrogênio na borracha a 27 ° C é 1,8 ⋅ 10   - 10 m 2 / s .

Passo 1

Fala aí! Tudo beleza? Vamos resolver essa questãozinha juntos!

Bom, pra começar vamos supor que estamos em condições estacionárias, simetria cilíndrica e fluxo convectivo desprezível, podemos então aplicar a Lei de Fick:

N A ,   d i f f =   - D A B ⋅ A ⋅ d C A d r

Teremos então que:

∫ r 1 r 2 N A ,   d i f f ⋅ d r r =   - ∫ C A 1 C A 2 D A B ⋅ 2 ⋅ π ⋅ L ⋅ d C A

Logo, teremos:

N A ,   d i f f = D A B ⋅ 2 ⋅ π ⋅ L ⋅ C A 1 - C A 2 l n r 2 / r 1

Teremos que C A 2 = 0 , mas precisamos encontrar o C A 1 :

C A 1 = 2,28 ⋅ 2  

C A 1 = 4,56   m o l / m 3

Substituindo os dados que temos:

N A ,   d i f f = 1,8 ⋅ 10   - 10 ⋅ 2 ⋅ π ⋅ 1 ⋅ 4,56   -   0 l n 5,5 / 1,5

Teremos então:

N A ,   d i f f = 3,969 ⋅ 10   - 9   m o l / s

ou

N A ,   d i f f = 1,429 ⋅ 10   - 5   m o l / h

Prontinho!

Resposta

N A ,   d i f f = 1,429 ⋅ 10   - 5   m o l / h

Exercício Resolvido #5

USP - Fenômenos de transporte III

Esboce a linha OM referenciada à reta de equilíbrio para a operação L → G .

Passo 1

Nessa questão nós vamos fazer a linha de equilíbrio para uma mudança do estado líquido para o estado gasoso, vamos lá!

Pra isso nós vamos usar a teoria das duas resistências, e pra começar vamos supor que a nossa solução é diluída, ou seja, a reta em equilíbrio é dada por:

y A i = m ⋅ x A i

Então o fluxo da fase líquida, será:

N A ,   z = k x ⋅ x A L - x A i

E o fluxo da fase gasosa, vai ser:

N A ,   z = k y ⋅ y A i - y A G

Levando em conta a teoria das duas resistências, vamos ter:

- k x k y = y A G   -   y A i x A L   -   x A i

Então, se a gente conhecer as composições do soluto na interface ( x A i , y A i ), podemos montar o gráfico que será muito útil para a determinação dos coeficientes individuais envolvidos na operação de transferência de massa em um determinado ponto do equipamento de separação.

Além disso, a inclinação da reta é a mesma para qualquer ponto da altura do equipamento, por conta da hipótese de a solução ser diluída, que assumimos lá em cima!

Nosso gráfico será:

Show de bolinhas!

Resposta

Passo 1.

Exercício Resolvido #6

USP - Fenômenos de transporte III - Professor Gerônimo

Construa as curvas de solubilidade (equilíbrio) para os seguintes sistemas:

  1. Amônia-água na temperatura de 30°C e 1 atm.
  2. S O 2 -água na temperatura de 20°C e 1 atm.
  3. Por intermédio de uma estimativa para m , procure mostrar qual fase controlará o processo de separação do soluto A nas situações apresentadas nos itens a e b.
  4. A partir do resultado obtido no item b, determine a relação k x k y para um certo ponto da torre com: x A L = 4,0 ⋅ 10 - 3 e y A G = 1,0 ⋅ 10 - 3 .

Dados:Amônia-água na temperatura de 30°C e 1 atm

S O 2 - água na temperatura de 20°C e 1 atm

Passo 1

Temos algumas letrinhas para resolver, vamos nessa! Começando pelos dados da letra a, e já resolvendo a letra c, em conjunto.

Vamos começar montando o gráfico com os valores dados e fazendo regressão linear para conseguir o valor de m .

Fazendo a regressão linear, na calculadora, vamos ter que:

m = 1,7338

Sendo assim, temos que:

y A i = 1,7338 ⋅ x A i

Bom, sabemos que a amônia é muito solúvel em água. E o nosso valor de m é pequeno, isso nos indica que é a fase gasosa que vai controlar o processo de separação, nas condições que foram dadas.

Passo 2

Agora vamos para os dados da letra b, mas já resolvendo a letra c também! Montando o gráfico, temos:

Fazendo a regressão linear, temos:

m = 33,73

Sendo assim, temos que:

y A i = 33,73 ⋅ x A i

Agora nós temos o valor de m muito grande, isso indica pra gente que a fase líquida vai controlar o processo de separação.

Passo 3

Agora vamos resolver a letra d, fazendo a relação k x k y para o ponto da torre x A L = 4,0 ⋅ 10 - 3 e y A G = 1,0 ⋅ 10 - 3 , temos que:

- k x k y = y A G   -   y A i x A L   -   x A i

Substituindo o ponto dado, ficamos com:

- k x k y = 1,0 ⋅ 10 - 3   -   33,73 ⋅ x A i 4,0 ⋅ 10 - 3   -   y A i 33,73

Agora vamos substituir cada um dos pontos da letra b, em x A i e y A i , montando uma tabela, teremos:

Finalizamos mais uma! Show!

Resposta

  1. Passo 1.
  2. Passo 2.
  3. Para o caso a, temos m = 1,7338 , como o valor de m é pequeno, a fase gasosa que vai controlar o processo de separação. Já para o caso b, m = 33,73 , o valor de m é muito grande, ou seja, fase líquida vai controlar o processo de separação.
  4. Passo 3.

Exercício Resolvido #7

USP - Fenômenos de transporte III - Professor Gerônimo

Para um sistema diluído em que o componente A é transferido da fase líquida à gasosa (torres de desabsorção), a relação de equilíbrio é dada por y A i = 0,75 ⋅ x A i . Em um certo ponto do equipamento experimental, o líquido contém 90% em mols de A e a composição de A nas fase gasosa é de 45% em mols. O coeficiente individual de transferência de massa do filme gasoso é 2,7 ⋅ 10 - 3   k g m o l / m 2 . s . △ y A e a resistência individual da fase gasosa é 60% da global. Determine:

  1. O coeficiente global K y ;
  2. As concentrações interfaciais de A nas duas fases;
  3. O fluxo molar de A.

Passo 1

Fala aí! Vamos começar anotando os dados que o enunciado deu pra gente, ok?

Coeficiente da fase gasosa: k y = 2,7 ⋅ 10 - 3   k g m o l / m 2 . s . △ y A

Reta de equilíbrio: y A i = 0,75 ⋅ x A i

Frações molares, no gás y A G = 0,45 , e no líquido, x A L = 0,90

Agora vamos para as continhas! Começando pela letra a, que quer o coeficiente global! Pra achar ele vamos lembrar que o enunciado disse que a resistência individual da fase gasosa é 60% da global, isso quer dizer que:

1 k y = 0,60 ⋅ 1 K y

Opa! Então vamos ter:

K y = 0,60 ⋅ k y

E substituindo o coeficiente individual da fase gasosa temos:

K y = 0,60 ⋅ 2,7 ⋅ 10 - 3

K y = 1,62 ⋅ 10 - 3   k g m o l / m 2 . s . △ y A

Passo 2

Na letra b, precisamos encontrar as concentrações nas duas fases, ou seja, ele quer o x A i e o y A i , pra isso vamos usar a teoria das duas resistências, assim:

- k x k y = y A G   -   y A i x A L   -   x A i

Substituindo os valores e sendo y A i = 0,75 ⋅ x A i , vamos ter:

- k x 2,7 ⋅ 10 - 3 = 0,45   -   0,75 ⋅ x A i 0,90   -   x A i

Opa! Precisamos encontrar o valor de k x antes, podemos entrar ele usando essa equação aqui:

1 K y = 1 k y + m k x

Substituindo os valores, teremos:

1 1,62 ⋅ 10 - 3 = 1 2,7 ⋅ 10 - 3 + 0,75 k x

k x = 3,04 ⋅ 10 - 3 k g m o l / m 2 . s . △ y A

Voltando na equação anterior, agora substituindo o valor de k x , ficamos com:

- 3,04 ⋅ 10 - 3 2,7 ⋅ 10 - 3 = 0,45   -   0,75 ⋅ x A i 0,90   -   x A i

x A i = 0,78

E podemos encontrar o y A i , assim:

y A i = 0,75 ⋅ 0,78

y A i = 0,585

Passo 3

Pra fechar, vamos encontrar o fluxo! Como estamos trabalhando com a fase líquida para a gasosa, podemos usar a seguinte equação para encontrar o fluxo:

N A ,   z = k x ⋅ x A L - x A i

Temos todos esses dados! Substituindo, ficamos com:

N A ,   z = 3,04 ⋅ 10 - 3 ⋅ 0,9 - 0,78

N A ,   z = 3,648 ⋅ 10 - 4   k g m o l / m 2 . s

Show de bolinhas! Terminamos!

Resposta

  1. K y = 1,62 ⋅ 10 - 3   k g m o l / m 2 . s . △ y A
  2. x A i = 0,78 e y A i = 0,585
  3. N A ,   z = 3,648 ⋅ 10 - 4   k g m o l / m 2 . s

Exercício Resolvido #8

Adaptado de USP - Fenômenos de transporte III - Professor Gerônimo

Construiu-se uma torre de recheios na intenção de absorver C O 2 do ar, utilizando-se água pura a 20°C como solvente e com velocidade superficial igual a 0,013 m/s, assim como anéis de Raschig cerâmicos de 13 mm. Considerando que o dióxido de carbono esteja diluído em relação aos inertes das duas fases e sabendo que a fase líquida é que controla a operação, estime o coeficiente volumétrico individual de transferência de massa utilizando a correlação de Normam, apresentada abaixo:

k x a = 530 ⋅ D A B L ⋅ ρ L M L ⋅ u L v L 0,75 ⋅ S c L   1 / 2

Dados: g   =   9,81   m / s 2 e visto o C O 2 estar diluído em água, as propriedades da corrente líquida serão tomadas como sendo às da água, ρ L = 998,2   k g / m 3 , v L = 1,01 ⋅ 10 - 6   m 2 / s , σ L = 72,47 ⋅ 10 - 3   N / m , M L = 18,015   g / g m o l e D A B L = 1,69 ⋅ 10 - 9   m 2 / s .

Passo 1

O enunciado pediu pra gente encontrar o coeficiente volumétrico de transferência de massa, com a correlação dada, e nos deu alguns dados… Então vamos lá!

Para usar a correlação de Normam:

k x a = 530 ⋅ D A B L ⋅ ρ L M L ⋅ u L v L 0,75 ⋅ S c L   1 / 2

Precisamos encontrar o Número de Schmidt, S c L , podemos achar ele assim:

S c L = v L D A B L

Substituindo os dados que temos:

S c L = 1,01 ⋅ 10 - 6 1,69 ⋅ 10 - 9 = 597,63

Show! Agora temos todos os parâmetros que precisamos! Vamos utilizar então a correlação dada, substituindo os nossos dados:

k x a = 530 ⋅ 1,69 ⋅ 10 - 9 ⋅ 998,2 18,015 ⋅ 0,013 1,01 ⋅ 10 - 6 0,75 ⋅ 597,63 1 / 2

O coeficiente volumétrico individual de transferência de massa, pela correlação de Normam, será:

k x a = 1,466   k g m o l / m 3 / s

Prontinho!

Resposta

k x a = 1,466   k g m o l / m 3 / s