Difusão em Regime Transiente
Teoria
Vamos juntos para mais um tópico! Se ligou que estamos saindo do regime permanente, né? Mas o que vai mudar na nossa vida com esse tal de Regime Transiente?
Dá uma olhada aqui, temos um recipiente com um líquido qualquer dentro dele, temos uma concentração inicial () e uma concentração final ().
O que aconteceu é que, nesse exemplo, a concentração diminuiu com o passar do tempo... Esse poderia ser um exemplo simples de um problema transiente, beleza?
Ou seja, aqui a gente vai ver como podemos lidar quando as condições do nosso problema estão variando com o tempo.
No regime transiente, a transferência de massa em geral quer dizer liberação ou acúmulo de uma espécie em um meio, fazendo com que a concentração mude ao longo do tempo. Então temos que a concentração será uma função do tempo:
Logo, nós temos que:
Ou seja, se o regime é transiente quando a gente fizer o balanço de massa, a gente não pode mais desprezar o termo de concentração em função do tempo. Vamos então considerar que o transporte de massa está acontecendo só por difusão (sem convecção), o nosso balanço vai ficar assim:
Aqui as nossas equações vão ficar um pouquinho mais complexas... Agora a gente vai ter derivadas espaciais, com relação ao espaço, e derivadas temporais, com relação ao tempo. E para resolver elas, a gente vai precisar de algumas simplificações que vão nos ajudar, elas geralmente são dadas no problema, as principais são:
- Geometria simples;
- Condições de início (tempo) e de contorno (espaço);
- Coeficiente de difusão () constante;
Considerando ainda que não está tendo reação química e que estamos em um problema unidimensional , fazendo as manipulações necessárias, com o conceito da 1ª Lei de Fick, temos então a expressão que define a 2ª Lei de Fick:
Ela também pode ser expressa em termos da concentração mássica, que ficaria assim:
Beleza! Mas como resolver esse tipo de EDO? Bom, pra isso vamos precisar usar alguns artifícios!
Difusão transiente em um meio semi infinito
Pensa numa lagoa, a superfície dela a gente sabe qual é, até porque a gente consegue ver. Mas e o fundo? Não dá nem pra imaginar, né? Ela pode ser tanto rasinha quanto muito funda.
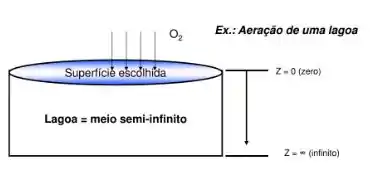
Beleza, e o que eu posso querer achar aqui?
Bom, usando as expressões que a gente já pode encontrar:
- O perfil de concentração, da mesma forma que já vimos ali em cima;
- O fluxo de mols transferidos em certo instante de tempo;
- O fluxo médio dentro de um intervalo de tempo;
- A taxa de mols transferida também em um intervalo;
Então a gente vai ver uma solução geral para o sólido semi-infinito, dos três tópicos que estão na nossa lista! Vamos lá!
Para encontrar o perfil de concentração vamos precisar admitir as seguintes condições de contorno:
Condição de Contorno Temporal:
Ela diz pra gente que quando , ou seja, no instante inicial, todo sistema está na concentração inicial.
Condição de Contorno Espacial:
E aqui ela está dizendo que quando estivermos na posição inicial, à variação da concentração ali será zero, e quando a gente tiver na superfície, a concentração será igual à concentração superficial.
Aplicando essas condições de contorno, nós vamos ficar com a seguinte relação:
Viu que ali tem um ? Ele é como a gente representa a função erro, pra achar seus valores podemos usar essa tabela aqui:
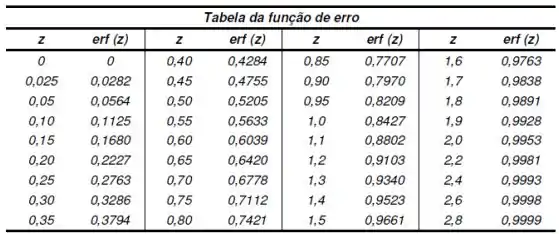
Onde é todo mundo que está dentro dos parênteses da função ... Se por acaso o valor que estivermos procurando não aparecer aí, vamos precisar interpolar belezinha?!
Pra calcular o Fluxo de mols transferidos no instante t:
A partir disso se obtém que:
Para calcular o Fluxo médio no intervalo de 0 a t:
Para calcular a Massa total transferida em um intervalo de tempo:
Onde é a taxa de moles transferidos e S é a superfície em que tá rolando a transferência de massa.
é a massa total transferida entre o intervalo 0 e t.
Agora que vimos tudo isso, vamos praticar!
Difusão transiente em um meio semi infinito
Beleza, e o que eu posso querer achar aqui?
Exercícios Resolvidos
Exercício Resolvido #1
Transferência de calor e massa - 4ª Edição - Çengel e Ghajar
Quando a densidade de uma espécie A em um meio semi-infinito é conhecida no ínicio e na superfície, explique como você determinaria a concentração da espécie A em determinado local e momento.
Passo 1
Fala aí! Vamos de questão teórica para fortalecer os conhecimentos? Partiu!
Bom, o enunciado já começa dizendo que a gente tem a densidade no início, , e a densidade na superfície, , né?
Opa! Vamos puxar da memória essa relação aqui, olha só:
Tendo as densidades, bem como o local, o tempo e o coeficiente de difusão… Essa seria uma maneira de conseguir determinar a concentração da espécie A, , beleza?
Prontinho! Ele só queria saber como a gente calcularia mesmo!
Resposta
Exercício Resolvido #2
Transferência de calor e massa - 4ª Edição - Çengel e Ghajar
Na análise da difusão de massa transiente, podemos tratar a difusão de um sólido em outro sólido de espessura finita (como a difusão de carbono em um componente de aço comum) como o processo de difusão em um meio semi-infinito? Explique.
Passo 1
Opa! Vamos de teoria!
Essa questão é aquela que a gente para, avalia e pensa… Boa pergunta!! haha
Vamos responder ela então! Para isso vamos ter em mente que quando temos difusão de dois sólidos, ela só vai afetar a camada mais superficial deles, beleza?
Opa! Acabamos de responder a questão… Se estamos em uma camada fina da superfície do outro sólido, é como se a difusão estivesse acontecendo realmente em um meio semi-infinito, tranquilo?
Mandamos bem!
Resposta
Sim, pois quando temos difusão de dois sólidos, ela só vai afetar a camada mais superficial deles podendo ser tratado então como um meio semi-infinito.
Exercício Resolvido #3
Elaboração própria.
Como podemos identificar um meio semi infinito?
Passo 1
Bom, pra começar, o que precisamos ter para considerar um sólido em um meio semi-infinito?
A gente pode até pensar que ele tem que necessariamente ser um sólido muitooo grande… Mas não é bem isso não!
Podemos considerar como um meio semi infinito todo sólido, com qualquer tamanho e forma, que possua a profundidade de penetração muito menor que a espessura dele, beleza?
Aí dá a impressão de infinito! Show de bola, né? Mas e o que é essa profundidade de penetração? Ela é a localização do nosso que está no perfil de concentração da superfície do sólido.
Prontinho!
Resposta
Passo 1.
Exercício Resolvido #4
UFPR - Difusão em Sólidos - Professor Adriano Scheid
Considere o método de endurecimento do aço obtido a partir de processo de difusão de carbono (cementação). O aço a ser cementado apresenta de carbono na composição nominal, e será tratado na temperatura de . A atmosfera do forno de cementação apresenta potencial de carbono de . Calcule o tempo necessário para que o aço tenha de carbono a de profundidade. O coeficiente de difusão para o carbono no ferro é de . A peça apresenta espessura semi-infinita.
Passo 1
Vamos resolver essa questão aí juntinhos? Partiu!
Bom, pra gente não se enrolar vamo começar anotando tudo o que foi dado, beleza?
Beleza! Quem a gente precisa encontrar aqui é o tempo, certo? Para isso a gente pode usar essa relação aqui, olha só:
Substituindo nossos dados, ficamos com:
Vamos ficar com:
Vish! Deu ruim! O , está dentro da função erro!
Relaxa! A gente pode fazer uma interpolação, ok? Vem comigo!
Passo 2
Precisamos achar um , tal que , tranquilo?
Então vamos usar dois valores, um abaixo e outro acima pra gente descobrir quem será esse , olha só:
Interpolando vamos ter que:
Teremos então:
Show! Mas nosso é tudo que estava dentro da função erro, certo? Então temos que:
Logo:
Manipulando essa equação:
O tempo será então:
ou
Uhul! Conseguimos!
Resposta
Exercício Resolvido #5
USP - Unidade 7 Difusão - Exercícios
É feita a difusão de boro numa pastilha de silício durante a . A pastilha de silício inicialmente é isenta de boro. Qual será a profundidade abaixo da superfície na qual a concentração em boro será de , se a concentração de boro na superfície for mantida constante e igual a ?
Dados:
- Solução da 2ª Lei de Fick para difusão não estacionária para as condições de contorno do exercício:
- Coeficiente de difusão do B no Si a :
Passo 1
E aí belezinha? Vamos resolver mais essa!
Olha o enunciado deu aquela ajuda, hein? Esses dados aí vão nos facilitar bastante!
Bom, vamo começar anotando tudo o que foi dado, show?
Olha só! O enunciado já deu até a fórmula pra gente usar, mas olhando rápido a gente pode achar que tá faltando o , né? Mas não tá não, sabe porquê? O enunciado fala que a pastilha de silício inicialmente é isenta de boro… Opa! Isso quer dizer que:
Tranquilo? Agora partiu continhas!
Passo 2
Substituindo apenas o lado esquerdo na equação, temos:
Vamos ficar com:
Agora a gente sabe quanto tem que dá essa função , né? Então vamos ver na tabela que foi dada pra achar quem é o … Lembrando que é toda galera que fica dentro da função . Vamos lá!
Nosso valor de , está entre esses dois valores aí… Ops! Vamos precisar interpolar!
A gente pode montar assim, olha só:
Interpolando vamos ter que:
Teremos então:
Opa! Então isso quer dizer que:
E substituindo os outros dados que temos:
Rearranjando, ficaremos com:
Nossa profundidade será:
ou
Show de bola! Arrasamos!
Resposta
Exercício Resolvido #6
Adaptado de USP - Cinética das Reações - Introdução
Uma peça de aço com concentração inicial de carbono é exposta a por a um gás que mantém a concentração na superfície da peça num valor constante . Calcular a concentração de carbono para , sabendo-se que .
Passo 1
Opa! Partiu resolver outra questão! Vamos nessa!
O enunciado pede pra gente encontrar a concentração do carbono, e ele nos dá as seguintes informações:
Para achar a concentração podemos usar a equação:
Já que temos todos os dados, vamos lá achar!
Ficaremos com:
Calculando a função erro, teremos:
Continuando nossas continhas, temos:
Logo, nossa concentração será:
Show de bolinhas! Arrasamos!
Resposta
Exercício Resolvido #7
Callister, W.D. Materials Science and Engineering: An Introduction. 8ª Ed.
Determinar o tempo de carburação necessário para ancorar uma concentração de carbono de em uma posição de em uma liga de ferro-carbono que contenha inicialmente. A concentração da superfície deve ser mantida em e o tratamento deve ser conduzido em .
Dados: , ,
Passo 1
Partiu resolver mais uma! Estamos indo bem! O enunciado quer que a gente encontre o tempo de carburação nas condições dadas… Vamos começar anotando nossos dados, ok?
Bom, vamos usar a equação que relaciona os nossos dados com o que queremos… Essa equação é a segunda Lei de Fick:
Opa! De cara a gente tá vendo que tá faltando o coeficiente de difusão pra gente achar o tempo, né? Vamos achar ele com a seguinte equação:
Substituindo os dados do enunciado:
Então o coeficiente de difusão será:
Agora sim vamos para a 2ª Lei de Fick!
Passo 2
Substituindo apenas o lado esquerdo na equação, vamos ter:
Vamos ficar com:
Agora vamos usar essa tabelinha aqui pra achar o valor de e descobrir o tempo que estamos procurando:
Eita! Olha só nosso valor de não está na tabela… Precisamos interpolar! Vamos nessa:
Vamos ter então:
Ficamos com:
Isso quer dizer:
Substituindo nossos dados:
Rearranjando, ficaremos com:
O tempo que buscamos é:
ou
Uhull!! Arrasamos!
Resposta
Exercício Resolvido #8
USP - Unidade 7 Difusão - Exercícios
Deseja-se difundir o metal A numa barra de metal B a partir de um filme de A depositado em uma face da barra de B, conforme indicado na figura abaixo. Após um tratamento a por , a concentração A a uma distância de a partir da interface é de . Qual deveria ser a temperatura para que a mesma concentração ( A) fosse atingida em uma posição de a partir da interface, supondo o mesmo tempo de tratamento? Considerar as hipóteses e condições de contorno apresentadas abaixo.
Hipóteses e condições de contorno:
- A concentração inicial de A em B é igual a é constante ao longo do corpo B.
- Nenhum átomo de B atinge a extremidade da barra de metal B oposta à face que recebeu o depósito de metal A, ou seja, a concentração de A nessa extremidade da barra de B é igual a durante todo o tratamento térmico de difusão.
- A concentração de A na interface AB é mantida constante durante todo o tempo de tratamento térmico de difusão e é igual a .
- A difusão de B em A pode ser considerada desprezível nas condições de tratamento térmico.
Equações:
- Utilizar a seguinte solução para a 2ª Lei de Fick para difusão não estacionária:
- A equação para o coeficiente de difusão é a seguinte:
Dados:
Passo 1
Opa! Fala aí! Essa parece cabeluda, né? Relaxa que nós damos conta juntos!
Olha só, o enunciado nos mostra duas situações diferentes, temos a parte do tratamento 1 e do tratamento 2, vamos anotar nossos dados para cada um deles:
Beleza! Agora usando as condições de contorno que foram dadas, onde e são constantes, isso quer dizer que todo o lado esquerdo da função é constante:
constante
Sendo assim, temos que:
constante
E mesmo sofrendo tratamentos diferentes, essa constante nos dois tratamentos serão iguais! Logo podemos dizer que:
Passo 2
Se as funções são iguais, então o que está dentro delas também é:
Opa! Se os tempos são iguais, então temos que:
O coeficiente do tratamento 1, podemos encontrar pois temos todos os dados, certo?
Para o tratamento 2 não podemos fazer isso! Porque não temos a temperatura, que é justamente o que estamos procurando, ok? Mas relaxa! Agora vamos voltar na relação que fizemos ali em cima e vamos conseguir achá-la!
Vamos ter então que:
Passo 3
E agora pra achar a temperatura? Como vamos fazer?
Opa! Podemos usar a relação do próprio coeficiente de difusão! Se liga só:
Temos então que:
Rearranjando vamos ter:
E tirando o dos dois lados, temos:
Sendo assim, a temperatura no tratamento 2, será:
ou
Prontinho! Demos conta de tudo!
Resposta
Exercício Resolvido #9
Fundamentos de transferência de massa - Cremasco - 2ª Edição
Uma bacia rasa contendo água destilada é posta subitamente em um ambiente contendo a e durante . Sabendo que nessas condições a solubilidade do na água é de , encontre a concentração mássica do a ; e a partir da interface gás-líquido.
Dado:
Passo 1
Vamos para mais uma! Precisamos encontrar a concentração mássica para os diferentes que o enunciado nos deu. Vamos usar a seguinte equação:
Como estamos trabalhando com água destilada, a concentração mássica inicial do dissolvido será zero, então, substituindo tudo que temos, a nossa equação vai ficar com essa carinha aqui:
Beleza! Agora vamos fazer a conta para , teremos:
Agora precisamos encontrar a função erro, olha só:
Vamos usar essa tabela como ajuda:
Precisamos interpolar, teremos:
--------------
---------
--------
---------
Vamos ficar então com:
Teremos:
Nossa função então será:
Passo 2
Agora vamos fazer o mesmo para :
Agora precisamos encontrar a função erro, olha só:
Usando a tabela:
Interpolando, teremos:
--------------
---------
--------
---------
Vamos ficar então com:
Ficamos com:
Nossa função então será:
Passo 3
Agora é a vez do :
A função erro vai ficar:
Usando a tabela agora, vamos ter:
Interpolando, teremos:
--------------
---------
--------
---------
Ficamos com:
Ficamos com:
Nossa função fica:
Prontinho!! Encontramos os resultados para as três situações!
Resposta
Para :
Para :
Para :
Exercício Resolvido #10
Fundamentos de transferência de massa - Cremasco - 2ª Edição
Pretende-se cementar um aço com , mantendo-o em uma atmosfera com em alta temperatura, até que se atinja em uma profundidade de abaixo da superfície. Qual o tempo total de cementação se o coeficiente de difusão for ?
Passo 1
Fala aí! Vamos começar anotando todos os nossos dados, beleza?
Temos:
Precisamos encontrar o tempo, então vamos usar essa relação aqui:
Substituindo nossos dados no lado esquerdo, vamos ter:
Temos então que:
Pra achar o , vamos precisar da ajuda da tabela aqui de baixo:
Passo 2
Opa! Vai ser preciso interpolar! Então vamos lá, pegar um valor acima e outro abaixo do que queremos:
Vamos ficar então com:
Teremos:
Voltando para nossa equação, vamos ter:
Rearranjando:
Nosso tempo então será:
ou
Show de bolinhas!!
Resposta
Exercício Resolvido #11
Unicamp - Fenômenos de transporte - Aula 25
Um teste de incêndio é conduzido sobre uma grande massa de concreto inicialmente a uma temperatura de . A temperatura da superfície atinge instantaneamente. Estime o tempo requerido para que a temperatura a uma profundidade de atinja . O concreto pode ser considerado como um sólido semi-infinito.
Dados: , , ,
Passo 1
Fala aí! Vamos resolver essa questãozinha juntos! Bom, o enunciado já nos deu o bizu! Ele diz que o concreto pode ser considerado um sólido semi-infinito, então pra gente encontrar o tempo podemos usar a equação:
Substituindo nossos dados na esquerda da equação, temos:
Logo, nossa função erro tem que ser igual a:
Para saber quem é o termo , que fica dentro da função erro, vamos usar a seguinte tabela:
Nosso resultado não está aí, então vamos encontrar dois valores que nos permitam fazer uma interpolação.
Passo 2
Pegando um valor acima e um valor abaixo do que precisamos, vamos ter:
Interpolando vamos ter que:
Teremos então:
Opa! Então isso quer dizer que:
Substituindo nossos dados:
Rearrumando, ficamos com:
Temos então que:
ou
Prontinho!!
Resposta
Exercício Resolvido #12
Adaptado de Unicamp - Fenômenos de transporte
Em um processo de cementação de uma peça de aço, calcule o tempo necessário para que a da superfície seja alcançada a composição de . Suponha que a peça está sendo processada a e a composição na superfície é de .
Dado: , .
Passo 1
Vamos começar anotando todos os nossos dados, beleza?
Precisamos encontrar o tempo, então vamos usar essa relação aqui:
Substituindo nossos dados no lado esquerdo, vamos ter:
Temos então que:
Pra achar o , vamos precisar da ajuda da tabela aqui de baixo:
Passo 2
Vai ser preciso interpolar! Então vamos lá, pegar um valor acima e outro abaixo do que queremos:
Vamos ficar com:
Teremos então:
Voltando para nossa equação, vamos ter:
Rearranjando:
Nosso tempo então será:
ou
Conseguimos!
Resposta
Exercício Resolvido #13
Adaptado de Unicamp - Fenômenos de transporte
Em um processo de cementação de um aço, a superfície da peça é tratada à concentração de e a . Calcular a composição da peça em um ponto situado a da superfície após uma hora de processamento.
Dado: .
Passo 1
Precisamos encontrar a composição do aço, na distância que foi dada, então queremos encontrar:
Vamos começar anotando todos os nossos dados:
Podemos usar essa relação:
Substituindo nossos dados:
Temos então que:
Vamos usar a tabela para encontrar a função erro:
Passo 2
Vai ser preciso interpolar! Então vamos lá, pegar um valor acima e outro abaixo do que queremos:
Vamos ficar com:
Teremos:
Voltando para nossa equação, vamos ter:
A composição da peça será:
Prontinho!