Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 13.Problemas - Ex. 114
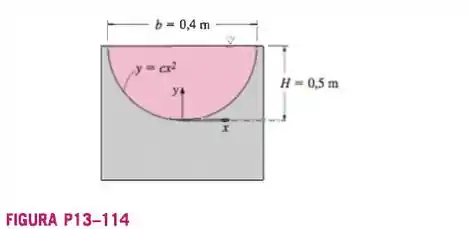
13-114 Considere o escoamento da água através do entalhe parabólico mostrado na Figura P13-128. Deduza uma relação para a vazão e calcule seu valor numérico para o caso ideal no
qual a velocidade de escoamento é dada pela equação de Toricelli .
Resposta: 0,246 m³/s
Passo 1
Muito bem, vamos ver o que temos aqui!!
A vazão volumétrica pode ser dada pela segunte integral:
O problema diz que o escoamento acontece em um canal parabólico. Puxando lá da matemática, temos uma equação para uma parábola com origem em e :
Pelo esqueminha que o problema nos da, podemos reconhecer o ponto do canto direito, quando e .
Isolando o e substituindo:
Ficamos então com:
Passo 2
Ok, mas como a gente faz pra chegar na vazão...?
Calma ai, estamos chegando perto!
Como a origem é em difirencial da área pode ser escrita como:
Substituindo :
Passo 3
O problema nos da a expressão para velocidade:
Podemos fazer:
Arrumando:
Como jájá vamos integrar, é interessante separar os valores constantes que conseguimos:
Passo 4
Integrando dos dois lados:
Já com a constante do lado de fora!!!
Resolvendo a integral, da esquerda:
Agora da direita:
Resolvendo a integral:
Substituindo achamos a expressão para vazão:
Agora a gente quer o valor numérico, substituindo:
Calculando:
Uhuuul!!! Prontinho!!