Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 13.Problemas - Ex. 89

13-89 Considere o escoamento uniforme da água em um canal largo com uma velocidade de 8 m/s e profundidade de escoamento de 0,8 m. Agora a água escoa sobre uma saliência com

30 cm de altura. Determine a variação (aumento ou diminuição) no nível da superfície da água sobre a saliência. Determine também se o escoamento sobre a saliência é subcrítico ou supercrítico.

Passo 1

Vamos láaa!! Pra começar com o pé direito, vamos desenhar um esqueminha!

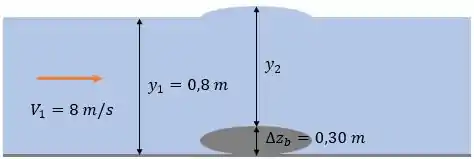
A gente quer descobrir quem a variação do nível da superfície da água, no nosso desenho ela é positiva, mas nada impede dela ser negativa, é só pra ilustrar! Beleza?!

A vazriação do nível fica:

Δ h = y 2 + Δ z b - y 1

Mas primeiro temos que ir atrás do y 2 !

Passo 2

Vamos primeiro calcular o número de Froude antes da saliência, para determinar o comportamento do escoamento:

F r 1 = V 1 g y 1 = 8 9,81 × 0,8 = 2,856  

Como F r 1 > 1   o escoamento é supercrítico, isso quer dizer que a profundidade do fluxo aumenta ao longo da saliência!

Agora, para achar y 2 , podemos usar a equação de energia:

y 2 3 - E s 1 - Δ z b y 2 2 + V 1 2 2 g y 1 2 = 0

Maaas, apareceram outras icógnitas que não temos!! Vamos encontrar primeiro a energia específica antes da saliência:

E s 1 = y 1 + V 1 2 2 g = 0,8 + 8 2 2 × 9,81 = 4,06   m

Substituindo na equação de energia:

y 2 3 - 4,06 - 0,30 y 2 2 + 8 2 2 × 9,81 0,8 2 = 0

Opaa, agora como a gente resolve isso?!

Passo 3

Para resolver esse problema, vamos usar o solver no Excel!

Escrevemos as variáveis, a equação e pedimos o solver pra um valor de y 2 para que a equação seja igual a zero:

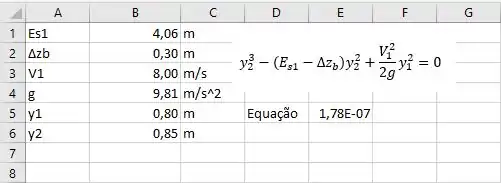
Achamos y 2 = 0,85   m

E finalmente podemos achar Δ h :

Δ h = 0,85 + 0,30 - 0,80 = 0,35   m

Uhuul, achamos uma resposta!!!

Passo 4

Agora a gente quer saber o comportamento do fluxo em cima da saliência. Para isso vamos calcular a energia específica crítica, E c , mas para isso precisamos conhecer y c :

y c = V ˙ 2 g b 2 1 3 = 0,8 2 × 8 2 9,81 1 3

Agora calculando E c :

E c = 3 2 y c = 3 2 × 1,61 = 2,42   m

Essa é a energia miníma, onde acontece a mudança de comportamento! Agora precisamos saber a energia específica depois da saliência:

E s 2 = E s 1 - Δ z b = 4,06 - 0,30 = 3,76   m

Agora vamos analisar! A energia específica vai de 4,06   m para 3,76   m e para que o escomanento passe de supercrítico pra crítico a energia deve atingir 2,42   m que é um valor menor que E s 2 !

Logo o escoamento continua supercrítico!!

Resposta

Δ h = 0,35   m

O escoamento é supercrítico.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

13-8C Em canais abertos, como é definido o raio hidráulico? Conhecendo o raio hidráulico, como o diâmetro hidráulico do canal pode ser determinado?
13-12C Observa-se que o escoamento em um canal aberto sofreu um salto hidráulico. O escoamento a montante do salto é necessariamente supercrítico? O escoamento a jusante do salto é necessariamente sub
13-18 Água a 10®C escoa em um canal circular com 3 m de diâmetro cheio até a metade a uma velocidade média de 2,5 m/s. Determine o raio hidráulico, o número de Reynolds e o regime de escoamento (lamin
13-16 Água a 15®C escoa de modo uniforme em um canal retangular com 2 m de largura a uma velocidade média de 4 m/s. Se a profundidade da água for 8 cm, determine se o escoamento será subcrítico ou sup
13-7C O que faz com que o escoamento em um canal aberto seja variado (ou não uniforme)? Em que o escoamento rapidamente variado difere do escoamento gradualmentc variado?