Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 13.Problemas - Ex. 95
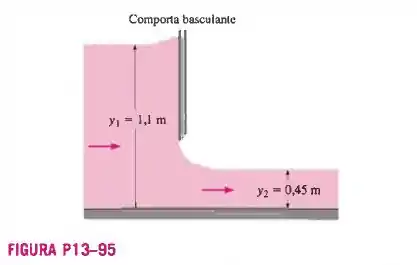
13-95 A vazão da água através de um canal com 5 m de largura (perpendicular ao papel) é controlada por uma comporta basculante. Se as profundidades de escoamento são medidas
como 1,1 e 0,45 m a montante e jusante das comportas, respectivamente, determine a vazão e o número de Froude a jusante da comporta.
Passo 1
Bora pra mais um exercício!?
Queremos a vaz��o e o número de Froude a jusante da comporta, ou seja depois da comporta! Mas uma coisa de cada vez, começando pela vazão!
O canal é horizontal, se considerarmos o atrito desprezível, então as energias específicas permanecem constantes:
Substituindo:
Opa, a gente pode substituir essas velocidades pela vazão, se a gente fizer...
Substituindo:
Substituindo os valores:
Simplificando:
Calculando:
Opaa, a primeira já foi!!
Passo 2
Agora a gente quer o número de Froude depois da comporta, :
Mas é:
Substituindo:
Agora podemos achar
Calculando:
Nesse caso o escoamento é supercrítico!!