Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 14.Problemas - Ex. 32
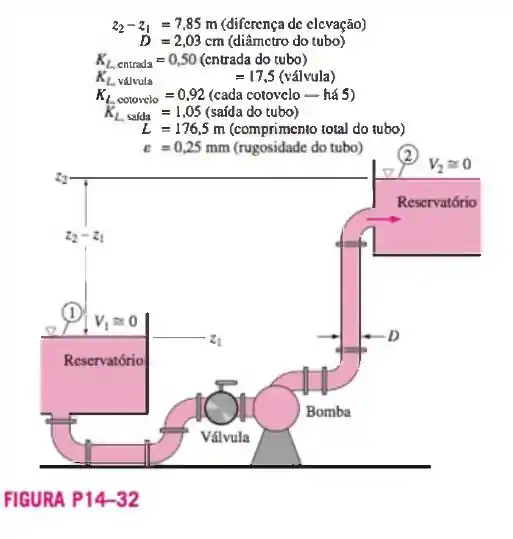
14-32 Uma bomba é usada para bombear água de um reservatório grande para outro reservatório grande a uma elevação maior. As superfícies livres de ambos os reservatórios estão expostas à pressão atmosférica, de acordo com a representação da Figura P14-32. As dimensões e os coeficientes de perda menor são fornecidos pela figura. O desempenho da bomba é aproximado pela expressão onde a carga de fechamento é de coluna d’água, o coeficiente , a carga disponível da bomba esta em unidades de metros de coluna d’água e a capacidade está em
unidades de litros por minuto (Lpm). Estime a capacidade fornecida pela bomba. Resposta: 11,6 Lpm.
Passo 1
E aiii, tudo bem?! Vamos fazer mais uma questãozinha iradoza de bombas?
Vem comigo então!!
A gente quer encontrar a vazão em que a bomba opera, então vamos começar escrever a equação de energia:
Vamos ver o que a gente consegue eliminar!
As superfícies e estão abertas para a atmosfera, portanto e como os reservatórios possuem grandes dimensões
Portanto:
A perda de carga é dada por:
Substituindo:
Passo 2
No ponto de operação temos:
E problema nos da:
A vazão é dada por:
Substituindo, ficamos com:
O problema nos da todos os dados, menos e o , o problema é que para calcular a velocidade a gente precisa do e para calcular o a gente precisa da velocidade!
Vamos ter então que usar um método interativo, mas antes disso vamos calcular o , que é a soma de todas as perdas menores dadas no enunciado:
Passo 3
Vamos então colocar todos os dados no EES:
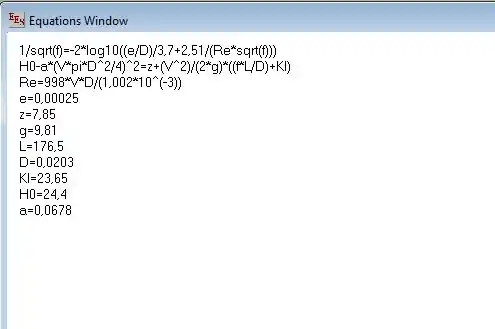
Resolvendo, achamos , podemos então calcular a vazão:
Ou: