Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 12.Problemas - Ex. 120

Nitrogênio entra em um trocador de calor com escoamento permanente a 150 kPa, 10 ℃ e 100 m / s , e recebe calor na quantidade de 150   k J / k g à medida que escoa através dele. O nitrogênio sai do trocador de calor a 100 kPa com uma velocidade de 2 00 m / s . Determine a pressão de estagnação e a temperatura do nitrogênio nos estados de entrada e saída.

Passo 1

Fala ai! Pra resolver essa questão primeiro temos que assumir algumas coisas já que estamos falando de escoamento de Fanno: estado estacionário, escoamento com atrito constante, gás ideal com propriedades contantes.

Vamos precisar saber algumas propriedades do nitrogênio:

k = 1,4

c p = 1,0 39 k J / k g . K  

Agora vamos imaginar um desenho:

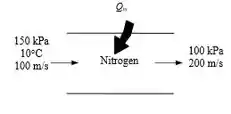
Como o nitrogênio que chega no trocador vai passar por um estado de estagnação, a temperatura e pressão vão ser então determinadas pela seguintes expressões:

T = T 0 - V ² 2 c p

P = P 0 T T 0 k / k - 1

Fazendo um balanço de energia a gente acha as condições na saída.

Passo 2

Como temos os dados do fluido de alimentação, podemos calcular a temperatura e pressão de estagnação na entrada! Sem esquecer de converter as unidades heim!

T = 10 - 10 0 2 2   x   10 39 = 14,8 ℃

P = 150 288 283 1,4 / 1,4 - 1 = 159   k P a

Passo 3

Pra descobrir a temperatura depois da troca térmica vamos usar um balanço de energia. Como estamos falando de estado estacionário, no nosso balanço não vai ter acúmulo e nem energia gerada, ficando então com essa cara aqui:

E e n t r a - E s a i = ∆ E s i s t e m a

Passando o termo de saída pro outro lado e substituindo cada termo por suas respectivas expressões:

q e n t r a = c p T 2 - T 1 + V 2 2 - V 1 2 2

150 = 1039 T 2 - 10 + 200 2 - 100 ² 2

T 2 = 139,9 ℃

Passo 4

Agora que temos a temperatura do nitrogênio depois do trocador de calor, vamos calcular a temperatura dele na saída, levando em consideração o ganho de velocidade. Vamos usar as mesmas expressões do passo 2.

T = T 0 - V 2 2 c p = 139,9 - 200 2 2 x 1039 = 159 ℃

P = P 0 T T 0 k / k - 1 = 100 T 432,3 413,1 1,4 / 1,4 - 1 = 117   k P a

Resposta

Na entrada:

T = 14,8 ℃

P = 159   k P a

Na saída:

T = 159 ℃

P = 117   k P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O que aconteceria se tentássemos desacelerar um fluido supersônico com um difusor divergente?
Como o parâmetro M a * difere do número de Mach M a ?
Explique por que a taxa máxima de escoamento por unidade de área de determinado gás depende apenas de P 0 / T 0 . Para um gás ideal com k = 1,4 e R = 0,287k J / k g K , encontre a constante a de forma
Ar entra em um bocal convergente-divergente a 0,8M P a com velocidade desprezível. Considerando o escoamento isentrópico, determine a contrapressão que resultará em um número de Mach de saída de 1,8 .
Nitrogênio entra em um bocal convergente-divergente a 700k P a e 400K com velocidade desprezível. Determine a velocidade crítica, a pressão, temperatura e massa específica no bocal.