5.101 Seguindo os passos para conveter a equação diferencial Eq. 5.31 (para m=1) em uma equação por diferenças (por exemplo, Eq. 5.37 para N=4), resolva
Para N=4, 8 e 16, e compare com a solução exata
Sugestão: Siga as regras para operações matriciais do Excel descritas no Problema 5.100. Apenas o lado direito das equações por diferenças mudarão, comparado ao método de solução da Eq. 5.31 (por exemplo, apenas o lado direito da Eq. 5.37 precisa de modificação).
Passo 1
Como ainda é uma equação diferencial de primeira ordem, ainda podemos usar a solução parecida com a do exemplo.
Com:
Então o sistema de equações fica, pra N=4:
Passo 2
Colocando tudo no excel:
Para N=4:
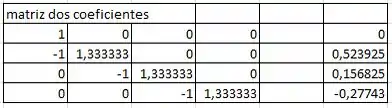
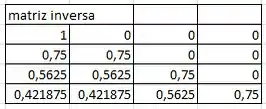
Para a matriz dos resultados que vai usar o =mmult, para multiplicar a matriz inversa com a ultima coluna da matriz dos coeficientes.. aí acha o resultado...
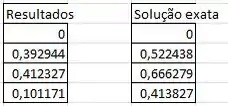
Passo 3
Para N=8:
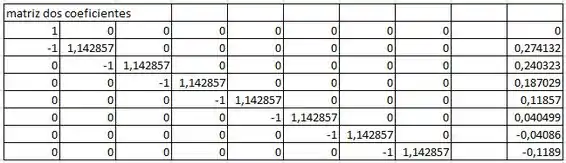

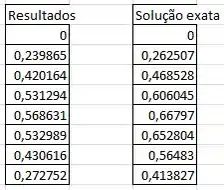
Passo 4
Para N=16:
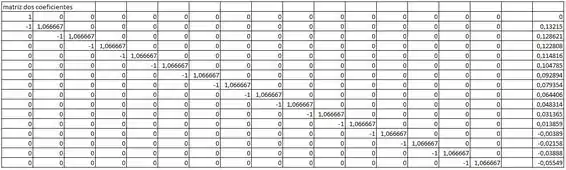
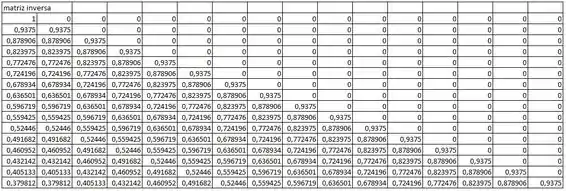

Passo 5

Resposta
São todas tabelas