Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 5.Problemas - Ex. 89
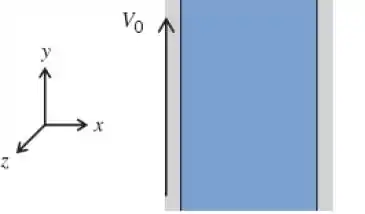
5.89 Considere um escoamento em regime permanente, laminar, incompressível, completamente desenvolvido, entre placas planas infinitas, comforme mostrado. O escoamento ocorre devido ao movimento da placa esquerda bem para como de um gradiente de pressão que é aplicado na direção y. Dadas as condições de que , w=0, e que a aceleração gravitacional age na direção negativa de y, prove que u=0 e que o gradiente de prssão na direção y deve ser constante.
Passo 1
Como foi dado que , isso significa que:
Como foi dado que o escoamento é completamente desenvolvido, que significa que , então:
E regime permanente significa que .
A equação da continuidade fica, então:
Mas, como u só depende de x:
Integrando, encontramos que:
Como a condição de contorno na parede é que a velocidade é igual a zero, então:
Como queríamos demonstrar.
Passo 2
Como e a gravidade está no sentido negativo da direção y, a componente x da equação de Navier-Stokes fica:
Então .
Como e a gravidade está no sentido negativo da direção y, a componente z da equação de Navier-Stokes fica:
Então .
A componente y da equação de Navier-Stokes fica:
Então:
Como também foi adotado regime permanente, então P só pode ser função de y ou constante. Porém olhando o lado direito da equação é razoável perceber que v ou é constante ou depende de x.
Mas matemáticamente é impossível uma função de y ser igual a uma função de x. Logo, só pode ser constante.