Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 5.Problemas - Ex. 65
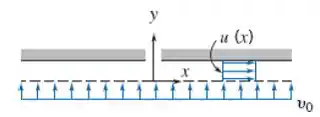
5.65 Ar escoa em uma folga estreita, de altura h, entre dois discos paralelos muito próximos, através de uma superfície porosa, conforme mostrado. Use um volume de controle, com superfície externa localizada na posição x, para mostrar que a velocidade uniforme na direção r e . Encontre uma expressão para a componente da velocidade na direção y. Avalie as componentes da aceleração de uma partícula fluida na folga.
Passo 1
Vamos considerar estado estacionário, fluido incompressível e fluxo uniforme em cada seção.
Usando a equação da continuidade pra achar uma expressão pra :
Como queríamos demonstrar.
Passo 2
Agora vamos usar a forma diferencial da equação da contiunidade para encontrar :
Separando as variáveis e integrando:
Onde C é a constante de integração.
Como quand , então:
Ficamos, então, com:
Passo 3
Baseado em tudo que assumimos lá em cima, a aceleração da partícula pode ser caculada com:
Na direção :
Calculando as derivadas parciais:
Então:
Passo 4
Na direção :
Calculando as derivadas parciais:
Então: