Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 5.Problemas - Ex. 85
5.85 Considere o escoamento induzido por pressão entre placas paralelas e estacionárias, separadas pela distância b. A coordenada y é medida a partir da placa inferior. O campo de velocidade é dado por . Obtenha uma expressão para a circulação sobre o contorno fechado de altura h e comprimento L. Avalie para h=b/2 e para h=b. Mostre que o mesmo resultado é obtido a partir da integral da área do Teorema de Stokes (Eq. 5.18).
Passo 1
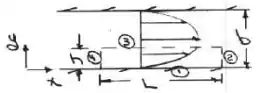
Considerando estado estacionário.
Da definição de circulação,
Podemos dividir a integral:
Como:
Então:
Passo 2
Para :
Para :
Resposta
Exercícios de Livros Relacionados
Em uma certa região de escoamento permanente, bidimensional, incompressível, o campo de velocidade é dado por V → = u , v = a x + b i → + - a y + c x j → . Mostre que essa região do escoamento pode se
Na deduaçao da equação de Bernoulli para regiões de escoamento sem viscosidade, reescrevemos a equação de Euler permanente, incompressível em uma forma mostrando que o gradiente de três termos escalar
Considere o escoamento de um fluido permanente, incompressível, bidimensional em um duto convergente, com paredes retas. A vazão em volume é V ˙ e a velocidade ocorre somente na direção radial, com ur
Em uma região irrotacional de escoamento, podemos escrever o vetor de velocidade como o gradiente da função potencial de velocidade escalar V → =∇ → ϕ . As componentes da velocidade em coordenadas cil
Água à temperatura de 20°C gira como um corpo rígido em relação ao eixo z em um recipiente cilíndrico giratório. Não há tensões viscosas pois a água move-se como um corpo sólido; portanto a equação de