Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 5.Problemas - Ex. 91

5.91 A componente x da velocidade em uma camada-limite laminar na água é aproximada por u = U   s e n   π y 2 δ , em que U = 3   m / s e δ = 2   m m . A componente y da velocidade é muito menor que u. Obtenha uma expressão para a força de cisalhamento resultante sobre um elemento fluido por unidade de volume na direção x. Calcule o seu valor máximo para este escoamento.

Passo 1

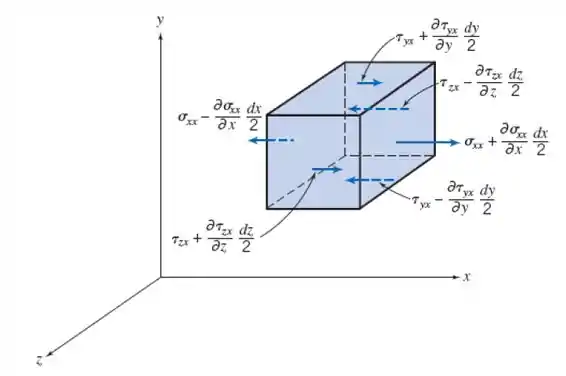
Considerando estado estacionário e como não tem compentente z, e a compontente y é muito pequena, então o diferencial da força de cisalhamento fica:

d F = τ y x + ∂ τ y x ∂ y d y 2 d x d z - τ y x - ∂ τ y x ∂ y d y 2 d x d z

d F = ∂ τ y x ∂ y d y 2 + ∂ τ y x ∂ y d y 2 d x d z

d F = d τ y x d x d z

Passo 2

Mas como é por unidade de volume:

d F d V = d τ y x d x d z d V

d F d V = d τ y x d x d z d x d y d z

d F d V = d τ y x d y

Sabemos também que tensão de cisalhamento é:

τ y x = μ d u d y

Substituindo: d F d V = d μ d u d y d y

d F d V = μ d 2 u d y 2

Passo 3

Com u = U   s e n   π y 2 δ :

d u d y = π 2 δ U cos ⁡ π y 2 δ

d 2 u d y 2 = - π 2 δ 2 U   s e n π y 2 δ

Então:

d F d V = - π 2 δ 2 U μ   s e n π y 2 δ

Passo 4

Pra achar o valor máximo podemos derivar e igualar a zero, maaaass como a função é seno... vamos só pensar um pouquinho que vai ser mais rápido...

A função seno tem valor máximo em 1... então queremos o valor de y que vai deixar s e n π y 2 δ igual a 1, certo? Que no caso é y = δ .

d F m á x d V = - π 2 δ 2 U μ   s e n π δ 2 δ

d F m á x d V = - π 2 δ 2 U μ   s e n π 2

d F m á x d V = - π 2 δ 2 U μ  

Substituindo os valores e como é água μ = 0,001 N s m 2 :

d F m á x d V = - π 2 0,002 2 3 0,001  

d F m á x d V = - 1,851   k N / m 3  

Resposta

d F m á x d V = - π 2 δ 2 U μ  

d F m á x d V = - 1,851   k N / m 3  

Ver Outros Exercícios desse livro