Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 5.Problemas - Ex. 98
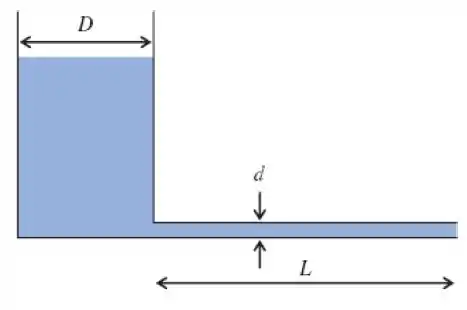
5.98 Um tanque com água (20°C) a uma profundidade inicial . O diâmetro do tanque é , e um tubo de diâmetro e comprimento , é anexado ao fundo do tanque. Para escoamento laminar um modelo razoável para o nível d água em função do tempo é
Usando os métodos de Euler com passos temporais de 12 min e de 6 min:
(a) Estime a profundidade de água após 120 min, e calcule os erros comparados com a solução exata
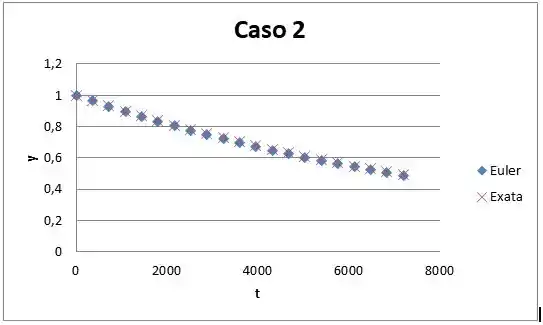
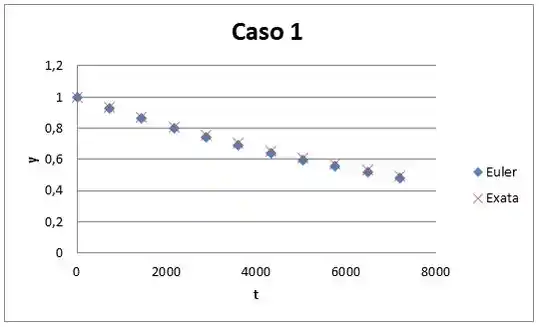
(b) Trace um gráfico com os resultados do método de Euler e da solução exata.
Passo 1
Usando o método de Euler:
Como,
e
E vamos pro nosso primeiro caso, onde o passo espacial é .
Então:
Colocando tudo isso nas células do excel (e tomando bastante cuidado com as unidades pra nao se atrapalhar e errar)
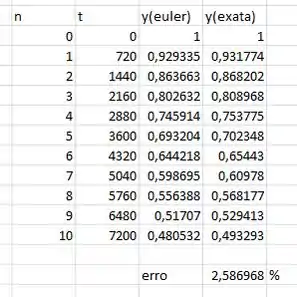
Para calcular o erro:
Passo 2
E vamos para o segundo caso, onde o passo espacial é .
Então:
Colocando tudo isso nas células do excel:
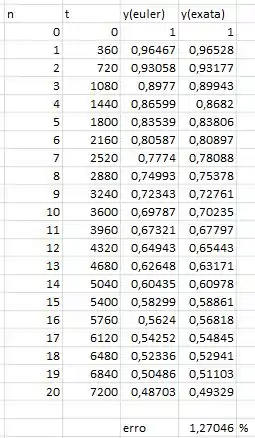
Para calcular o erro:
