Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 7.Problemas - Ex. 124
O abelhão pode ficar suspenso no ar à velocidade igual a zero, batendo as asas. Usando os dados do Problema, conceba uma teoria para asas móveis, em que a batida descendente seja modelada como uma placa plana curta normal ao escoamento e a batida ascendente seja como uma pluma, com arrasto aproximadamente igual a zero. Quantas batidas por segundo desse modelo de asa são necessárias para sustentar o peso do abelhão? (Medidas reais em abelhas mostram uma taxa de batidas de asas de .)
Passo 1
E aí, tudo bem? Bora matar essa questão!
Vamos fazer um esqueminha da nossa abelha para entender as variáveis!
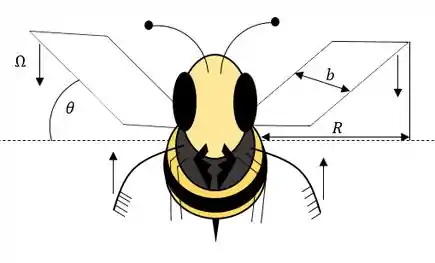
Vamos considerar que quando a asa tá subindo devido sua característica de pena, ela terá força de sustentação com valor .
E quando estiver descendo para compensar a ausência de força, cada asa irá produzir , para compensar ausência de sustentação durante a subida!
Passo 2
Assumindo a condição de placa plana curta, da tabela temos que:
Considerando um elemento de comprimento da asa da abelha, temos:
Lembrando que:
Logo:
Integrando tudo, temos que:
Passo 3
Para uma batida de asas completa temos:
Substituindo tudo na nossa equação:
Resolvendo pra
O valor é cerca de maior do que o valor Real, mas o valor encontrado se trata apenas de uma teoria pura!
Isso é tudo pessoal, conseguimos mais uma! \o/
Resposta
O valor é cerca de maior do que o valor medido, mas o valor encontrado se trata apenas de uma teoria pura!