Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 11.Problemas - Ex. 14

Em geral, como varia o coeficiente de arrasto com o número de Reynolds em (a) números de Reynolds baixo e moderado e (b) números de Reynolds altos ?

Passo 1

A questão quer saber a influência do número de Reynolds no coeficiente de arrasto em dois casos: no caso de números de Reynolds baixos e moderados e no caso de número de Reynolds altos .

Para número de Reynolds baixos o coeficiente de arrasto é inversamente proporcional ao número de Reynolds .

Ou seja, para , quanto maior o número de Reynolds , menor o coeficiente de arrasto .

Para número de Reynolds maiores, mas ainda menores que , a tendência geral do coeficiente de arrasto continua sendo de diminuir com o aumento do número de Reynolds.

Passo 2

Para número de Reynolds maiores que , o coeficiente de arrasto permanece praticamente constante com a variação do número de Reynolds . A figura abaixo mostra o caso geral que acontece para a maioria das geometrias de corpo. No entanto, os números presentes nesse gráfico são relativos ao escoamento sobre um disco perpendicular.

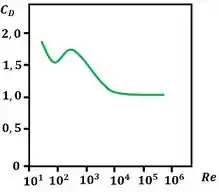
Resumindo, o coeficiente de arrasto diminui com o aumento do número de Reynolds para , mas em geral permanece constante para .

Resposta

O coeficiente de arrasto diminui com o aumento do número de Reynolds para .
Em geral, o coeficiente de arrasto permanece constante para .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Mostre que, se as Equações ( 7.70 ) e ( 7.71 ) são válidas, a razão máxima entre a sustentação e o arrasto ocorre quando C A = 2 C A ∞ . Quais são F S / F A m á x á e a para uma asa simétrica quando R

Em 2001, um avião comercial perdeu toda a potência durante um voo a 10.000m sobre o Oceano Atlântico, a cerca de 100k m da Ilha dos Açores. Os pilotos, com habilidade admirável, colocaram o avião em u

O abelhão pode ficar suspenso no ar à velocidade igual a zero, batendo as asas. Usando os dados do Problema7.123 , conceba uma teoria para asas móveis, em que a batida descendente seja modelada como u

Em voo de planeio (sem potência), a sustentação e o arrasto estão em equilíbrio com o peso. Mostre que, se não houver vento, a aeronave desce com um ângulo tan ⁡ θ ≈ a r r a s t o s u s t e n t a ç ã

80 – A bela expressão para a sustentação de um aerofólio bidimensional, eq. 8.72, surge da aplicação da transformação de Joukowski, ζ = z + a 2 z Em que, z = x + i y ;ζ = η + i β A constante a é uma e