Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 13.Problemas - Ex. 211

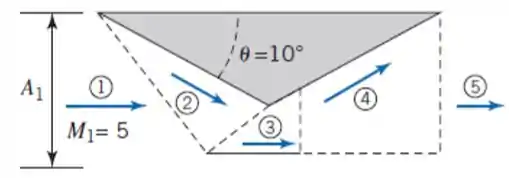
Uma aeronave voando a Mach 5, onde T 1 = 216,67   K . Choques oblíquos se formam no coletor de admissão antes de entrar na câmara de combustão 3. A razão de expansão do bocal é A 5 / A 4 = 5 . As áreas de entrada e de saída são iguais, A 1 = A 5 = 0,2   m 2 . Considerando escoamento isentrópico com M 2 = 4 , M 3 = 9,295 e M 4 = 1,26 , calcule o número de Mach na saída e a velocidade do jato de exaustão 5.

D i c a : Calcule as razões de temperatura em cada seção.

Passo 1

Calculando V 1 :

V 1 = M 1 k R T 1

Sendo:

M 1 = 5 ;

k = 1,4 ;

R = 287   N ⋅ m / k g ⋅ K ;

T 1 = 216,67   K .

Temos:

V 1 = 5 ⋅ 1,4 ⋅ 287 ⋅ 216,67

V 1 = 1475,3   m / s

Calculando a razão entre A 4 / A * :

A 4 A * = 1 M 4 1 + k - 1 2 M 4 2 k + 1 2 k + 1 2 k - 1  

Sendo:

M 4 = 1,26 ;

Temos:

A 4 A * = 1 1,26 1 + 1,4 - 1 2 ⋅ 1,26 2 1,4 + 1 2 1,4 + 1 2 1,4 - 1

A 4 A * = 1,05

Passo 2

Calculando a razão entre A 5 / A *   :

A 5 A * = A 5 A 4 ⋅ A 4 A *

Sendo:

A 5 A 4 = 5 .

Então:

A 5 A * = 5 ⋅ 1,05 = 5,25

Calculando M 5 :

A 5 A * = 1 M 5 1 + k - 1 2 M 5 2 k + 1 2 k + 1 2 k - 1

Substituindo:

5,25 = 1 M 5 1 + 1,4 - 1 2 M 5 2 1,4 + 1 2 1,4 + 1 2 1,4 - 1

M 5 = 3,23

Passo 3

Pela figura "Ângulo de deflexão oblíqua do choque", temos que:

Para M 1 = 5 , θ = 10 ° e β = 20 ° .

A componente normal do número Mach se dá:

M 1 n = M 1   s e n   β

M 1 n = 5 ⋅ s e n   20 °

M 1 n = 1,7

Calculando a razão de temperatura  T 2 / T 1 :

T 2 T 1 = 1 + k - 1 2 M 1 n 2 k M 1 n 2 - k - 1 2 k + 1 2 2 M 1 n 2

Substituindo os dados:

T 2 T 1 = 1 + 1,4 - 1 2 ⋅ 1,7 2 1,4 ⋅ 1,7 2 - 1,4 - 1 2 1,4 + 1 2 2 ⋅ 1,7 2

T 2 T 1 = 1,4 6

Calculando a razão de temperatura  T 3 / T 2 :

T 3 T 2 = 1 + k - 1 2 M 2 n 2 k M 2 n 2 - k - 1 2 k + 1 2 2 M 2 n 2

Sendo:

M 2 n = 4 ⋅ s e n   20 ° = 1,37 .

Temos:

T 3 T 2 = 1 + 1,4 - 1 2 ⋅ 1,37 2 1,4 ⋅ 1,37 2 - 1,4 - 1 2 1,4 + 1 2 2 ⋅ 1,37 2

T 3 T 2 = 1,23

Calculando a razão de temperatura  T 3 / T 2 :

T 4 T 3 = 1 + k - 1 2 M 3 n 2 k M 3 n 2 - k - 1 2 k + 1 2 2 M 3 n 2

Sendo:

M 3 n = 9,295 ⋅ s e n   20 ° = 3,18 .

Temos:

T 4 T 3   = 1 + 1,4 - 1 2 ⋅ 3,18 2 1,4 ⋅ 3,18 2 - 1,4 - 1 2 1,4 + 1 2 2 ⋅ 3,18 2

T 4 T 3 = 2,89

Passo 4

Calcule a razão de temperatura T 0 4 / T 4 :

T 0 4 T 4 = 1 + k - 1 2 M 4 2

Substituindo os dados:

T 0 4 T 4 = 1 + 1,4 - 1 2 ⋅ 1,26 2

T 0 4 T 4 = 1,32

Temos que T 0 5 T 0 4 = 1 , já que T 0 4 = T 0 5 .

Calcule a razão de temperatura T 0 5 / T 5 :

T 0 5 T 5 = 1 + k - 1 2 M 5 2

T 0 5 T 5 = 1 + 1,4 - 1 2 ⋅ 3,23 2

T 0 5 T 5 = 3,09

Passo 5

Considerando que:

T 5 T 1 = T 2 T 1 T 3 T 2 T 4 T 3   T 0 4 T 4 T 0 5 T 0 4 T 5 T 0 5

Então:

T 5 216,67 = 1,46 ⋅ 1,23 ⋅ 2,89 ⋅ 1,32 ⋅ 1 ⋅ 1 3,09

T 5 = 480,4   K

Calculando V 5 :

V 5 = M 5 k R T 5

V 5 = 3,23 ⋅ 1,4 ⋅ 287 ⋅ 480,4  

V 5 = 1419   m / s

Resposta

M 5 = 3,23

V 5 = 1419   m / s

Ver Outros Exercícios desse livro