Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 13.Problemas - Ex. 206

Determine o coeficiente de arrasto do aerofólio simétrico mostrado, com ângulo de ataque zero, para um número de Mach 2,0 no ar, cuja pressão estática e temperatura são 95   k P a e 0 ° C , respectivamente. Os ângulos inclusos no nariz e na cauda são ambos de 10 ° .

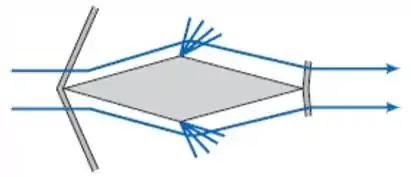
Passo 1

Começamos o problema sabendo que o aerofólio é simétrico em relação a qualquer um dos eixos, por isso apresentam características de choques semelhantes.

Para superfícies de ponta:

M 1 = 2 ;

θ u = 10 ° 2 = 5 °   .

Então:

tan ⁡ θ u = 2 cot ⁡ β u M 1 2   s e n 2   β u - 1 M 1 2 k + cos ⁡ 2 β u + 2

Sendo:

k = 1,4 .

Temos:

tan ⁡ 5 ° = 2 cot ⁡ β u 2 2   s e n 2   β u - 1 2 2 1,4 + cos ⁡ 2 β u + 2

β u = 34,5 °

Calculando M 1 n   s u p e r i o r :

M 1 n   s u p e r i o r = M 1   s e n   β u

M 1 n   s u p e r i o r = 2 ⋅ s e n   34,5 °

M 1 n   s u p e r i o r = 1,133

Calculamos p 2 pelas relações de pressão de choques oblíquos:

p 2   s u p e r i o r p 1 = 2 k k + 1 M 1 n   s u p e r i o r 2 - k - 1 k + 1

Sendo:

p 1 = 95   k P a .

Temos:

p 2   s u p e r i o r 95 = 2 ⋅ 1,4 1,4 + 1 ⋅ 1,133 2 - 1,4 - 1 1,4 + 1

p 2   ( s u p e r i o r ) = 125,4   k P a

Pela simetria:

p 2   ( s u p e r i o r ) = p 2   ( i n f e r i o r ) = 125,4   k P a

Passo 2

Borda direita:

Das relações de choques oblíquos:

M 2 n 2 = M 1 n 2 + 2 k - 1 2 k k - 1 M 1 n 2 - 1

Substituindo:

M 2 n 2 = 1,133 2 + 2 1,4 - 1 2 ⋅ 1,4 1,4 - 1 ⋅ 1,133 2 - 1

M 2 n = 0,891

Calculando M 2   s u p e r i o r :

M 2 n = M 2   ( s u p e r i o r )   s e n   ( β u - θ u )

0,891 = M 2   ( s u p e r i o r )   s e n   ( 34,5 ° - 5 ° )

M 2   ( s u p e r i o r ) = 1,82

Pelas funções de Prandtl Mayer:

ω 1 = k + 1 k - 1 tan - 1 ⁡ k - 1 k + 1 M 2   s u p e r i o r 2 - 1 - tan - 1 ⁡ M 2   s u p e r i o r 2 - 1

Substituindo:

ω 1   ( s u p e r i o r ) = 1,4 + 1 1,4 - 1 tan - 1 ⁡ 1,4 - 1 1,4 + 1 1,82 2 - 1 - tan - 1 ⁡ 1,82 2 - 1

ω 1   ( s u p e r i o r ) = 21,32 °

Passo 3

Na superfície da borda posterior:

θ = 10 ° .

ω 2   ( b o r d a   s u p e r i o r ) = ω 1   ( s u p e r i o r ) + 10 °

ω 2   ( b o r d a   s u p e r i o r ) = 21,32 ° + 10 °

ω 2   ( b o r d a   s u p e r i o r ) = 31,32 °

Novamente pelas funções de Prandtl Mayer, calculamos M 2 :

ω 2   ( b o r d a   s u p e r i o r ) = k + 1 k - 1 tan - 1 ⁡ k - 1 k + 1 M 2   b o r d a   s u p e r i o r 2 - 1 - tan - 1 ⁡ M 2   b o r d a   s u p e r i o r 2 - 1

Substituindo:

31,32 = 1,4 + 1 1,4 - 1 tan - 1 ⁡ 1,4 - 1 1,4 + 1 M 2   b o r d a   s u p e r i o r 2 - 1 - tan - 1 ⁡ M 2   b o r d a   s u p e r i o r 2 - 1

M 2   b o r d a   s u p e r i o r = 2,18

Das relações isentrópicas, calculamos p 0 2 :

p 0 2 p 2   ( s u p e r i o r ) = 1 + k - 1 2 M 2   s u p e r i o r 2 1 + k - 1 2 M 2   b o r d a   s u p e r i o r 2 k k - 1

Substituindo:

p 0 2 125,4 = 1 + 1,4 - 1 2 ⋅ 1,82 2 1 + 1,4 - 1 2 ⋅ 2,18 2 k k - 1

p 0 2 = 71,4   k P a

Assim:

p r e s s ã o   n a   b o r d a   s u p e r i o r = p r e s s ã o   n a   b o r d a   i n f e r i o r = 71,4   k P a

Calculando a força de arrasto:

F H = s ⋅ c 2 ⋅ tan ⁡ 3 ° p 2   s u p e r i o r + p 2   i n f e r i o r - p 2   b o r d a   s u p e r i o r + p 2   b o r d a   i n f e r i o r

F H = s ⋅ c 2 ⋅ 0,052 ⋅ 125,4 + 125,4 - 73,4 + 73,4

F H = 2,69 ⋅ s ⋅ c   k N

Passo 4

Sendo:

F H = F D

Temos:

C D = F D 1 2 ρ v 2 ⋅ s ⋅ c

Calculando ρ :

p = ρ R T

Sendo:

p = 95   k P a ;

R = 287   N ⋅ m / k g   ⋅ K ;

T = 0 ° C = 273   K .

Temos:

95 x 10 3 = ρ ⋅ 287 ⋅ 273

ρ = 1,21   k g / m 3

Calculando v :

v = M k R T

Substituindo:

v = 2 ⋅ 1,4 ⋅ 287 ⋅ 273

v = 662,3   m / s

Voltando ao coeficiente de arrasto:

C D = 2,69 ⋅ s ⋅ c 1 2 ⋅ 1,21 ⋅ 662,3 2 ⋅ s ⋅ c

C D = 0,010

Resposta

C D = 0,010

Ver Outros Exercícios desse livro