Projete um anemômetro de vento que utiliza arrasto aerodinâmico para mover ou defletir uma peça ou acoplamento, produzindo uma saída que pode ser relacionada com a velocidade do vento, para a faixa de a no ar-padrão. Considere três conceitos de projeto alternativos. Selecione o melhor conceito e prepare um projeto detalhado. Especifique a forma, tamanho real e material para cada componente. Quantifique a relação entre velocidade do vento e saída do anemômetro. Apresente resultados como uma “curva de calibração” da saída do anemômetro velocidade do vento. Discuta as razões pelas quais você rejeitou projetos alternativos e escolheu o conceito final do projeto.
Passo 1
Montando o esquema do anemômetro:
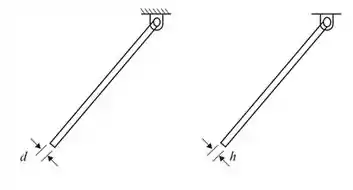
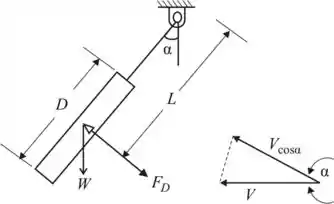
Equação do momento:
Sendo:
Temos:
Passo 2
Supondo na velocidade máxima do vento ():
Isolando :
Em temos ;
;
;
/
.
Temos:
Escolho o alumínio na Tabela A.1 (:
Passo 3
Relacionando velocidade do vento e saída do anemômetro:
Passo 4
Apresentando os resultados como uma “curva de calibração” da saída do anemômetro velocidade do vento:
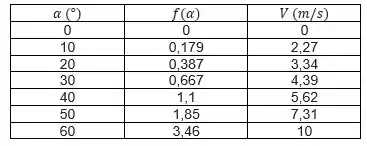

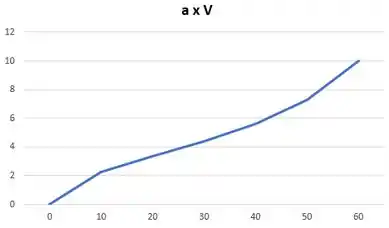
Passo 5
Os conceitos considerados incluíam um manômetro que detectava pressão de estagnação, uma ligação de paralelogramo que suporta um alvo vertical e a flexão de um membro fino na corrente de ar. Os três conceitos escolhidos foram variações sobre o tema de um único membro suspenso suportado por um único pivô e foram escolhidos devido a sua simplicidade.
A principal vantagem do conceito de alvo é que diferentes materiais podem ser usados para a haste e o alvo. Este conceito pode ser adaptado para fornecer o maior ângulo de deflexão para uma determinada velocidade do vento. Desse modo, este dispositivo deve ter a indicação mais precisa em baixa velocidade do vento.
Presume-se que a força de arrasto no alvo dependa do componente da velocidade do vento que age normalmente no alvo. Isso poderia ser melhorado usando dados experimentais reais para o coeficiente de arrasto de um disco no ângulo de ataque.