O agitador de uma máquina de lavar deve ser projetado. A potência, , requerida para o agitador deve ser correlacionada com a quantidade de água usada (indicada pela profundidade, , de água). A potência também depende do diâmetro do agitador, , da altura, , da velocidade angular máxima, , da frequência de oscilações, , da massa específica da água, , e da viscosidade da água, . Determine os parâmetros adimensionais que caracterizam este problema.
Passo 1
Heyy, vamos ver o que temos aqui? Nessa questão nos é dito que o poder de um agitador de máquina de lavar depende de vários parâmetros. E com eles vamos encontrar os grupos adimensionais. Vamos lá!
Passo 2
Para resolver essa questão vamos usar o procedimento de Buckingham.
![]()
Selecionando as dimensões primárias
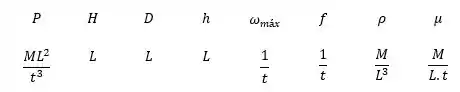
E os parâmetros repetidos:
![]()
Passo 3
Então temos grupos adimensionais e vamos configurar uma equação dimensional,
Somando os expoentes:
Temos que a solução do sistema é:
Então:
Passo 4
Para o segundo grupo temos,
Somando os expoentes:
Temos que a solução do sistema é:
Então:
Passo 5
Já os outros grupos podem ser encontrados por inspeção:
Podemos ainda conferir se está tudo certinho usando as dimensões primárias :