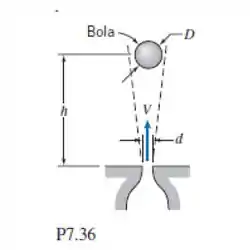
O esquema mostra um jato de ar descarregando verticalmente. Experiências mostram que uma bola colocada no jato fica suspensa em uma posição estável. A altura de equilíbrio da bola o jato depende de D, d, V, ρ, μ, e de W, em que W é o peso da bola. Análise dimensional é sugerida para correlacionar os dados experimentais. Determine os parâmetros que caracterizam este fenômeno.

Agora a gente vai listar as dimensões primárias desses parâmetros! A gente vai fazer isso usando se você quiser usar o e comparar a resposta final, tudo bem!

A gente usou as dimensões e , então:

Como vimos que temos que selecionar parâmetros dentro dos nossos parâmetros relevantes, que vão ser os parâmetros repetidos.

Relembando nossos parâmetros relevantes:

é o parâmetro dependente, então a gente já exclui ele!

Temos e com a mesma dimensão, vamos escolher o para ser um parâmetro repetido!

Entre os parâmetros relevantes que sobram, é interessante pegar os mais simples, dai já podemos tirar e .

Ficamos com:

A gente tem:

E:

Então ficamos com:

Logo vamos achar quatro grupos !

Agora sim, vamos encontrar o nosso primeiro grupo !!

Começando com o , onde vamos usar o:

Escrevendo suas dimensões básicas:

Equacionando:

Massa:

Comprimento:

Tempo:

Logo:

Substituindo , e , temos:

Organizando:

Para o a gente vai fazer relacionando com as variáveis repetidas! Só que a dimensão de é exatamente igual a dimensão de , então a relação vai ser a mesma, só precisamos substituir por :

Agora vamos de , dessa vez vamos descobrir a relação de com as variáveis repetidas:

Escrevendo suas dimensões básicas:

Equacionando:

Massa:

Comprimento:

Tempo:

Logo:

Substituindo

Organizando:

E finalmente, o último que é o com a relação de com os parâmetros repetidos:

Escrevendo suas dimensões básicas:

Equacionando:

Massa:

Comprimento:

Tempo:

Logo:

Substituindo

Organizando:

Uhuuuuul!!!