Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas - Ex. 56

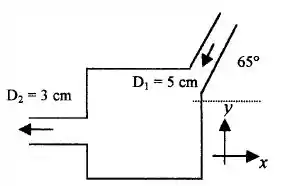
Água a 20°C escoa em regime permanente através da caixa abaixo, entrando na seção 1 a 2m/s. Calcule (a) a força horizontal e (b) a força vertical necessárias para manter a caixa parada contra o fluxo de quantidade de movimento.

Passo 1

E aí, minha galerinha! Tudo bem? Quero aqui te convidar pra encararmos mais um desafio de mecânica dos fluidos!!!

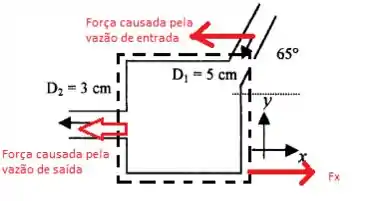
(a) Vamos fazer então o que se pede, que é primeiramente calcular a nossa força na direção horizontal, ou seja:

∑ F x = 0 → F x + m ˙ e u e , x - m ˙ s u s = 0

Passo 2

Vamos precisar lembrar que para um escoamento incompressível, temos que as vazões de entrada e saída devem ser iguais. Além disso, note que a velocidade u s = V 2 , enquanto isso, vamos precisar decompor a velocidade de entrada para obter sua componente na direção x.

u e , x = - V 1 c o s θ

Note que o sinal negativo foi colocado uma vez que a componente x está apontando para o sentido oposto do eixo x.

F x = m ˙ s u s - m ˙ e u e , x

Lembrando que as vazões mássicas são o produto entre a densidade do fluido, a velocidade de escoamento e a área transversal por onde esse fluido escoa. Como estamos tratando de FORÇAS, precisamos adotar os sinais (+) quando estivermos no sentido crescente do eixo x e (-) quando estivermos indo pro sentido negativo do eixo x.

F x = ρ V 2 A 2 - V 2 - ρ V 1 A 1 - V 1 c o s θ

Conhecemos a velocidade no ponto 1, então pelo balanço de massa, temos:

Q 1 = Q 2 → V 1 A 1 = V 2 A 2

V 1 π 4 D 1 2 = V 2 π 4 D 2 2 → V 2 = V 1 D 1 D 2 2 = 2 0,05 0,03 2 = 5 , 56   m / s

Substituindo os valores com ρ = 998   k g / m ³ e A 1 = π 4 D 1 2   e A 2 = π 4 D 2 2   e θ = 65 ° , vamos encontrar um valor de F x = 18,5   N

Passo 3

(b) A força vertical será feita usando o mesmo volume de controle, porém agora olhando somente para as forças na vertical, o que resultará em:

∑ F y = R y = - m ˙ e u e , y = - ρ V 1 A 1 - V 1 s e n θ

R y = - 998   x   2   x π 4 0,05 2 - 2   s e n 65 ° = 7,1   N

Resposta

  1. F x = 18,5   N
  2. F y = 7,1   N
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Explique a importância do teorema de transporte de Reynolds na mecânica dos fluidos e descreva como a equação do momento linear é obtida a partir dele.
Enuncie a primeira, segunda e terceira leis de Newton.
Um foguete no espaço (nenhum atrito ou resistência ao movimento) pode expelir gases a uma certa velocidade alta V em relação a si mesmo. V é o limite superior para velocidade final do foguete?
Como as forças de superfície surgem na análise do momento de um volume de controle? Como é possível minimizar o número de forças de superfície expostas durante a análise?
Expresse a segunda lei do movimento de Newton para pás rotativas. O que é possível dizer sobre a velocidade angular e o momento angular de um corpo não rígido em rotação de massa constante, se o torqu