Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas - Ex. 55
Na figura abaixo, o jato atinge a pá movendo-se para a direita à velocidade constante em um carrinho sem atrito. Calcule (a) a força requerida para conter o carrinho e (b) a potência P entregue ao carrinho. Encontre também a velocidade do carrinho para qual (c) a força é máxima e (d) a potência P é máxima.
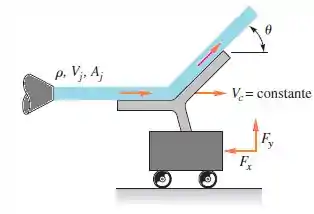
Passo 1
(a) Bem, esse exercício é um clássico na mecânica dos fluidos e eu estou aqui pra te ajudarrr!!
Então vamos observar o seguinte, se queremos calcular a força na direção x, então precisamos fazer um balanço de forças!!!
Primeiro vamos observar que, o jato atinge a pá em uma velocidade relativa de , afinal a pá está se movendo, então precisamos trabalhar com velocidade relativa.
Como o carrinho não sofre acelera, temos que o somatório das forças deve dar zero!
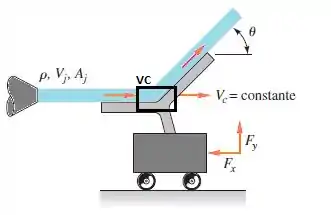
Note que precisamos decompor nossa velocidade de saída na direção x, certo?
Passo 2
A vazão mássica é constante porque estamos em uma física com fluido incompressível! Então podemos escrever que:
Sabemos que as velocidades de entrada e saída devem ser iguais, pois a área de seção transversal de escoamento se manteve ao longo do escoamento, logo:
Passo 3
A vazão mássica é dada pelo produto da vazão volumétrica pela densidade do fluido, então vamos escrever assim nossa equação de balanço de forças:
Passo 4
(b) A potência concedida ao carrinho é dada pela fórmula
Passo 5
(c) Para observar quando a força será máxima, vamos observar nossa equação para Fx
Podemos concluir então que quando Vc= 0, teremos que Fx será máxima.
Passo 6
(d) A potência máxima acontece quando derivamos nossa equação em função da velocidade do carrinho e igualamos isso a zero.
Gerando o valor de